132o
126o
108o
102o
Correct answer is B
In the diagram; 108° + x + x = 180° (sum of angle in a triangle)
108° + 2x = 180°
x = 180° - 108°
= 72°
x = \(\frac{72^o}{2}\)
= 36°
(Angle between tangent and a chord through the point of contact)
Hence, angle PTN = 90 + 36
= 126°
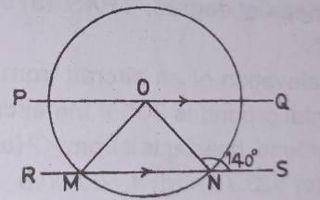
In the diagram, O is the centre. If PQ//RS and ∠ONS = 140°, find the size of ∠POM.
40o
50o
60o
80o
Correct answer is A
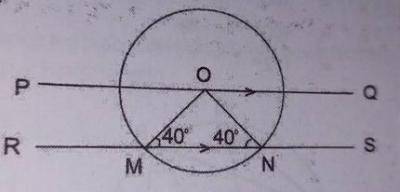
In the diagram above,
∠MNO = 140° and angles on a straight line is 180°
: ∠NMO = (180 - 140)° = 40°
Hence; ∠POM = 40° ( alternate angle ∠S)
14cm
7m
3\(\frac{1}{2}\)m
1\(\frac{3}{4}\)m
Correct answer is C
Volume of rectangular tank = L x B x H
= 2 x 7 x 11
= 154cm3
volume of cylindrical tank = \(\pi r^2h\)
154 = \(\frac{22}{7} \times r^2 \times 4\)
r2 = \(\frac{154 \times 7}{22 \times 4}\)
= \(\frac{49}{4}\)
r = \(\sqrt{\frac{49}{4}} = \frac{7}{2}\)
= 3\(\frac{1}{2}\)m
3.0cm
3.5cm
4.0cm
4.5cm
Correct answer is B
Using V = \(\frac{3}{1} \pi r^2h\),
so, 38\(\frac{1}{2} = \frac{1}{3} \times \frac{22}{7} \times r^2 \times 3\)
\(\frac{77}{2} = \frac{22}{7} \times r^2\)
r2 = \(\frac{77 \times 7}{2 \times 22}\)
r2 = \(\frac{49}{4}\)
Hence, r = \(\sqrt{\frac{49}{4}}\)
= 3\(\frac{1}{2}\)
x2 - x - 3 = 0
x2 - 3x - 1 = 0
x2 - 3x - 3 = 0
x2 + 3x - 1 = 0
Correct answer is B
Given; y = x2 - x - 2, y = 2x - 1
Using y = y, gives
x2 - x - 2 = 2x - 1
x2 - 3x - 2 + 1 = 0
therefore, x2 - 3x - 1 = 0
WAEC Subjects
Aptitude Tests