WAEC Mathematics Past Questions & Answers - Page 77

Cost price CP of the 100 oranges = \(\frac{100}{5}\) x N40.00

selling price SP of the 100 oranges = \(\frac{100}{20}\) x N120

= N600.00

so, profit or loss per cent

= \(\frac{SP - CP}{CP}\) x 100%

= \(\frac{600 - 800}{800}\) x 100%

= \(\frac{-200}{800}\) x 100%

Hence, loss per cent = 25%

R \(\alpha\) D²

R = D²K

R = 4 Litres when D = 15cm

thus; 4 = 15²k

4 = 225k

k = \(\frac{4}{225}\)

This gives R = \(\frac{4D^2}{225}\)

Where R = 9litres

equation gives

9 = \(\frac{4D^2}{225}\)

9 x 225 = 4d²

D² = \(\frac{9 \times 225}{4}\)

D = \(\sqrt{9 \times 225}{4}\)

= \(\frac{3 \times 15}{2}\)

= 22\(\frac{1}{2}\)km

Let x represent the entire farmland

then, \(\frac{2}{5}\)x + \(\frac{1}{3}\)[x - \(\frac{2}{3}x\)] + M = x

Where M represents the part of the farmland used for growing maize, continuing

\(\frac{2}{5}\)x + \(\frac{1}{3}\)x [1 - \(\frac{2}{3}x\)] + M = x

\(\frac{2}{5}x + \frac{1}{3}\)x [\(\frac{3}{5}\)] + M = x

\(\frac{2}{5}\)x + \(\frac{1x}{5}\) + M = x

\(\frac{3x}{5} + M = x\)

M = x - \(\frac{2}{5}\)x

= x[1 - \(\frac{3}{5}\)]

= x[\(\frac{2}{5}\)] = \(\frac{2x}{5}\)

Hence the part of the land used for growing maize is

\(\frac{2}{5}\)

\(\frac{3x - y}{xy} - \frac{2x + 3y}{2xy} + \frac{1}{2}\)

= \(\frac{2(3x - y) - 1(2x + 3y) + xy}{2xy}\)

= \(\frac{6x - 2y - 2x - 3y + xy}{2xy}\)

= \(\frac{4x - 5y + xy}{2xy}\)

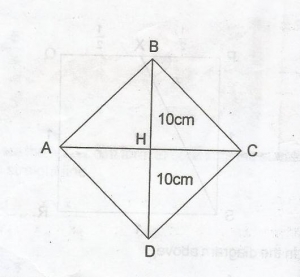
Diagonal |AC| = (2x + 1)cm

In the diagram,area of \(\Delta\)ABC

is \(\frac{110}{2}\) = \(\frac{1}{2}\) x |AC| x |HB|

55 = \(\frac{1}{2}\) x (2x + 1) x 10

55 = (2x + 1)5

55 = 10x + 5

55 - 5 = 10x

50 = 10x

x = \(\frac{50}{10}\)

= 5.0