Le 2,250,000.00
Le 22,700,000.00
Le 3,600,000.00
Le 4,500,000.00
Correct answer is C
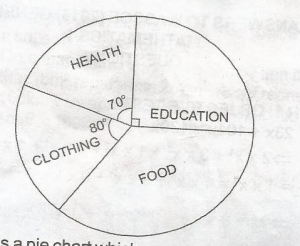
sectoral angle representing food
= 360o - (80 + 70 + 90)o
= 120o
Amount spent on food
= \(\frac{\tect{sectoral angle}}{360^o}\) x Le 10,800,000
= Le 3,600,000
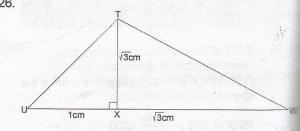
In the diagram, TX is perpendicular to UW, |UX| = 1cm and |TX| = |WX| = \(\sqrt{3}\)cm. Find UTW
135o
105o
75o
60o
Correct answer is C
In \(\Delta\) UXT, tan\(\alpha\) = \(\frac{1}{\sqrt{3}}\)
\(\alpha\) = tan-1(\(\frac{1}{\sqrt{3}}\))
= 30o
In \(\Delta\)WXT, tan\(\beta\) \(\frac{\sqrt{3}}{\sqrt{3}}\) = 1
\(\beta\) = tan-1(1) = 45o
Hence, < UTW = \(\alpha\) + \(\beta\)
= 30o + 45o = 75o
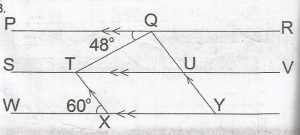
In the diagram, PR||SV||WY|, TX||QY|, < PQT = 48o and < TXW = 60o.Find < TQU.
120o
108o
72o
60o
Correct answer is C
In the diagram, < TUQ + 60o(corresp. angles)
< QTU = 48o (alternate angles)
< QU + 60o + 48o = 180o(sum of angles of a \(\Delta\))
< TQU = 180o - 108o
= 72o
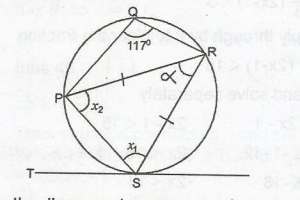
In the diagram, TS is a tangent to the circle at S. |PR| and < PQR = 177o. Calculate < PST.
54o
44o
34o
27o
Correct answer is A
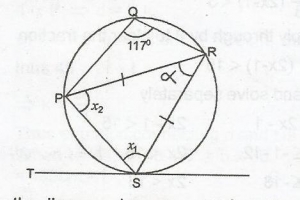
In the diagram above, x1 = 180o - 117o = 63o(opposite angles of a cyclic quad.)
x1 = x2 (base angles of isos. \(\Delta\))
x1 + x2 + \(\alpha\) = 180o (sum of angles of a \(\Delta\)
63o + 63o + \(\alpha\) = 180o
\(\alpha\) = 180o - (63 + 63)o
= 54o
4.5m
6.0m
7.5m
9.0m
Correct answer is C
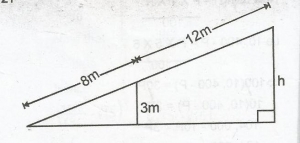
By similar triangles, \(\frac{8}{3}\) = \(\frac{8 + 12}{h}\)
\(\frac{8}{3} = \frac{20}{h}\)
h = \(\frac{3 \times 20}{8}\)
= 7.5m
WAEC Subjects
Aptitude Tests