Processing math: 100%

WAEC Mathematics Past Questions & Answers - Page 65

321.

Simplify; 2 $\frac{1}{4} \times 3\frac{1}{2} \div 4 \frac{3}{8}$

$\frac{5}{9}$

1 $\frac{1}{5}$

1 $\frac{1}{4}$

1 $\frac{4}{5}$

View answer & explanation

Correct answer is D

2 $\frac{1}{4} \times 3\frac{1}{2} \div 4 \frac{3}{8}$

= $\frac{9}{4} \times \frac{7}{2} \div \frac{35}{8}$

= $\frac{9}{4} \times \frac{7}{2} \div \frac{8}{35}$

= $\frac{9}{5}$

= 1 $\frac{4}{5}$

322.

Find the value of x for which $32_{four} = 22_x$

three

five

six

seven

View answer & explanation

Correct answer is C

$32_4 = 22_x$

$3 \times 4^1 + 2 \times 4^o$ = $2 \times x^1 + 2 \times x^o$

12 + 2 x 1 = 2x + 2 x 1

14 = 2x + 2

14 - 2 = 2x

12 = 2x

x = $\frac{12}{2}$

x = 6

323.

Evaluate: $(64^{\frac{1}{2}} + 125^{\frac{1}{3}})^2$

121

144

169

196

View answer & explanation

Correct answer is C

$[64^{\frac{1}{2}} + 125^{\frac{1}{3}}]^2$ = $[\sqrt{64} + \sqrt[3] {125}]^2$

$[8 + 5]^2$ = $[13]^2$

= 169

324.

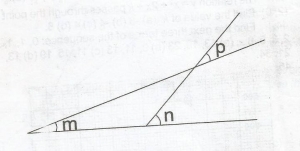
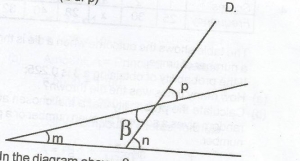
From the diagram, which of the following is true?

m + n + p = 180^o

m + n = 180^o

m = p + n

n = m + p

View answer & explanation

Correct answer is D

In the diagram, $\beta$ = p(vertically opposite angles)

m + $\beta$ = n(sum of interior opp. angles)

m + p = n

325.

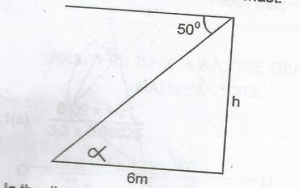
An object is 6m away from the base of a mast. If the angle of depression of the object from the top of the mast is 50^o, find, correct to 2 decimal places, the height of the mast.

8.60m

7.83m

7.51m

7.15m

View answer & explanation

Correct answer is D

In the diagram give, $\alpha$ 50^o(alternative angles)

tan $\alpha$ = $\frac{h}{6}$

h = 6tan $\alpha$

= 6tan 50^o

= 6 x 1.1918

= 7.1508

= 7.15m (2d.p)

WAEC Subjects

Literature in English

Islamic Religious Knowledge

Christian Religious Knowledge

Aptitude Tests

Puzzles Questions and Answers

Data Interpretation Questions and Answers

Verbal Reasoning Questions and Answers

Nigeria General Knowledge Questions and Answers

Typing Speed and Accuracy Test

Personality Test

Microsoft Office Questions and Answers

Numerical Reasoning Questions and Answers

Situational Judgement Questions and Answers

Logical Reasoning Questions and Answers

Spatial Reasoning Questions and Answers

Abstract Reasoning Questions and Answers

Quantitative Reasoning Questions and Answers

See all →

View latest jobs in Nigeria today