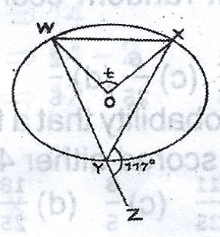
Find the value of t in the diagram
63\(^o\)
117\(^o\)
126\(^o\)
234\(^o\)
Correct answer is C
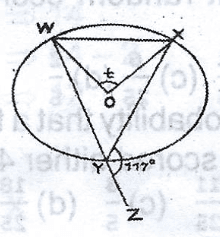
In the diagram,
\(\alpha\) = 180\(^o\) - 177\(^o\) (angles on a straight line)
\(\alpha\) = 63\(^o\)
t = 2 x 63\(^o\) (angle at centre = 2 x angle at circum)
= 126\(^o\)
Find the mean deviation of 20, 30, 25, 40, 35, 50, 45, 40, 20 and 45
8
9
10
12
Correct answer is B
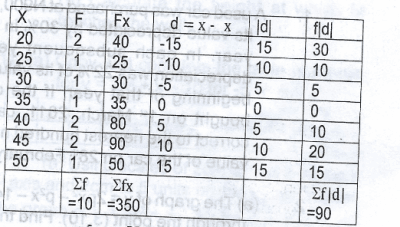
Mean = \(\frac{\sum f x}{\sum f}\)
= \(\frac{350}{10}\)
= 35
= \(\frac{\sum f |d|}{\sum f}\)
= \(\frac{90}{10}\)
= 9
Find the median of 2, 1, 0, 3, 1, 1, 4, 0, 1 and 2
0.0
0.5
1.0
1.5
Correct answer is C
First arrange the numbers in ascending order of magnitude; 0, 0, 1, 1, 1, 1, 2, 2, 3, 4
Counting from the right, the fifth number is 1
Counting from the left, the fifth number is 1
Hence, median = \(frac{1 + 1}{2}\)
= \(\frac{2}{2}\)
= 1
If P and Q are two statements, under what condition would p|q be false?
If p is true and q is true
If p is true and q is false
If p is false and q is false
If p is false and q is true
Correct answer is B
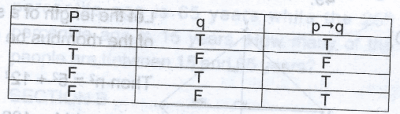
From the truth table above, p \(\to\) q would be false if p is true and q is false
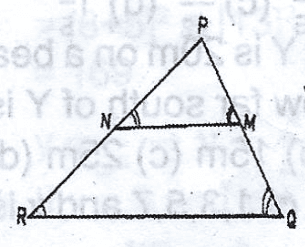
In the diagram, which of the following ratios is equal to \(\frac{|PN|}{|PQ|}\)?
\(\frac{|PN|}{|PR|}\)
\(\frac{|PM|}{|PQ|}\)
\(\frac{|PM|}{|PR|}\)
\(\frac{|PR|}{|PQ|}\)
Correct answer is C
\(\frac{|PN|}{|PQ|}\) = \(\frac{|PM|}{|PR|}\)
WAEC Subjects
Aptitude Tests