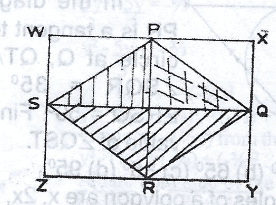
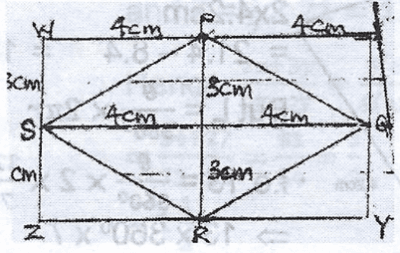
WAEC Mathematics Past Questions & Answers

286.

The solution of x + 2 $\geq$ 2x + 1 is illustrated

iii

View answer & explanation

Correct answer is A

x + 2 $\geq$ 2x + 1

x - 2x $\geq$ 1 - 2

-x $\geq$ -1

$\frac{-x}{-1}$ $\geq$ $\frac{-1}{-1}$

x $\leq$ 1

287.

In the diagram, WXYZ is a rectangle with diamension 8cm by 6cm. P, Q, R and S are the midpoints of the rectangle as shown. Using this information calculate the area of the part of the rectangle that is not shaded

25cm $^2$

24cm $^2$

16cm $^2$

12cm $^2$

View answer & explanation

Correct answer is B

Area of shaded part = 2 x area of $\bigtriangleup$ SPQ

= 2 x $\frac{1}{2}$ 8 x 3 =24cm

Hence, area of the unshaded part of the rectangle = area of rectangle - area of shaded part

= 8 x 6 - 24

= 48 - 24

= 24 cm $^2$

288.

In the diagram, PS and RS are tangents to the circle centre O. ∠PSR = 70°, ∠POR = m, and ∠PSR =n. Find ( m + n ).

110 $^o$

135 $^o$

165 $^o$

225 $^o$

View answer & explanation

Correct answer is C

In the diagram,

Thus, m = 2 x 55 $^o$ (is a bisector of obtuse

m = 110 $^o$

n = $\frac{1}{2}$ x 110 $^o$ (angle at centre = 2 x angle at circum)

n = 55 $^o$

m + n = 110 + 55 = 165 $^o$

289.

In the diagram, WXYZ is a rectangle with dimension 8cm by 6cm. P, Q, R and S are the midpoints of the sides of the rectangle as shown. Using this information, what type of quadrilateral is the shaded region?

Trapezium

Prism

Rectangle

Rhombus

View answer & explanation

Correct answer is D

No explanation has been provided for this answer.

290.

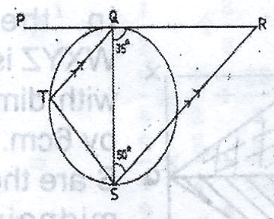
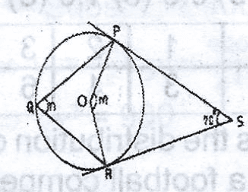
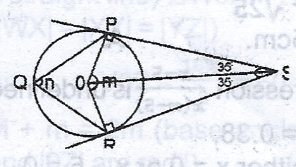
In the diagram, PR is a tangent to the circle at Q, QT//RS,

40 $^o$

65 $^o$

85 $^o$

95 $^o$

View answer & explanation

Correct answer is D

In the diagram,

a = 50 $^o$ (alternate angles)

b $_1$ + a 35 $^o$ = 180 $^o$ (sum of angles on a straight line)

i.e; b $_1$ + 50 $^o$ + 35 $^o$

= 180v

b $_1$ + 180 $^o$ - 85 $^o$ = 90 $^o$

But b $_2$ = $b_1$ = 95 $^o$ (angles in alternate segement)

<QST = b $_2$ = 95 $^o$

WAEC Subjects

Literature in English

Islamic Religious Knowledge

Christian Religious Knowledge

Aptitude Tests

Puzzles Questions and Answers

Data Interpretation Questions and Answers

Microsoft Office Questions and Answers

Spatial Reasoning Questions and Answers

Logical Reasoning Questions and Answers

Nigeria General Knowledge Questions and Answers

Personality Test

Situational Judgement Questions and Answers

Abstract Reasoning Questions and Answers

Quantitative Reasoning Questions and Answers

Typing Speed and Accuracy Test

Verbal Reasoning Questions and Answers

Numerical Reasoning Questions and Answers

See all →

View latest jobs in Nigeria today

WAEC Mathematics Past Questions & Answers - Page 58

WAEC Subjects

Aptitude Tests