In how many ways can a committee of 3 women and 2 men be chosen from a group of 7 men and 5 women?
500
350
720
210
Correct answer is D
For choosing, its different 'combinations'
Options - 7 men, 5 women
To pick - 2 men, 3 women
∴ The number of ways to choose a committee of 3 women and 2 men from a group of 7 men and 5 women is:
=\(^5C_3 \times ^7C_2\)
=\(\frac{5\times4\times3}{3\times2}\times\frac{7\times6}{2\times1}\)
=\(10\times21\)
=210
2.0
1.4
1.8
1.6
Correct answer is B
n = 5
x̄ = \(\frac{∑x}{n} = \frac{85 + 84 + 83 + 86 + 87}{5} = \frac{425}{5} = 85\)
| \(x\) | \(x - x̄\) | \((x - x̄)^2\) |
| 85 | 0 | 0 |
| 84 | -1 | 1 |
| 83 | -2 | 4 |
| 86 | 1 | 1 |
| 87 | 2 | 4 |
| \(\Sigma(x - x̄)^2 = 10\) |
\(S.D = √\frac{∑(x - x̄ )}{n} = √\frac{10}{5}\)
∴ S.D = √2 =1.4
\(5\frac{2}{5}\)
\(4\frac{1}{5}\)
\(13\frac{1}{2}\)
\(6\frac{3}{4}\)
Correct answer is A
Sum to infinity of a G.P when /r/ < 1 = \(\frac{a}{1 - r}\)
a = \(\frac{9}{2},r = \frac{T_2}{T_1} = \frac{3}{4} + \frac{9}{2}\)
r = \(\frac{3}{4} \times \frac{2}{9} = \frac{1}{6}\)
\(S_∞ = \frac{\frac{9}{2}}{1-\frac{1}{6}} = \frac{\frac{9}{2}}{\frac{5}{6}} = \frac{27}{5}\)
\(\therefore S_∞ = 5\frac{2}{5}\)
2.0
3.0
2.5
4.0
Correct answer is C
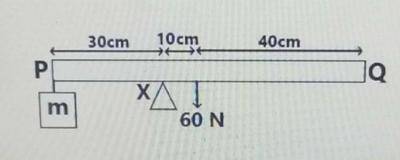
∑ clock wise moments =∑ anti clock wise moments
= 60 x 10 = 30 x m
= 600 = 30 m
m = \(\frac{600}{30} = 20 N\)
W = mg ==> m = \(\frac{W}{g}\)
∴ m = \(\frac{20}{10} = 2kg\)
If \(f : x → 2 tan x\) and \(g : x → √(x^2 + 8), find ( g o f )(45^o)\)
4
2√3
6
3√2
Correct answer is B
\(f : x → 2 tan x\)
\(g : x → √(x^2 + 8)\)
\(( g o f ) = √((2 tan x)^2 + 8)\)
\(( g o f )(45º) = √((2 tan 45º)^2 + 8)\)
= √(4 + 8) = √12
= √(4 x 3)
∴ 2√3
WAEC Subjects
Aptitude Tests