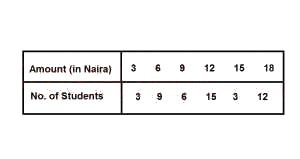
1,567.
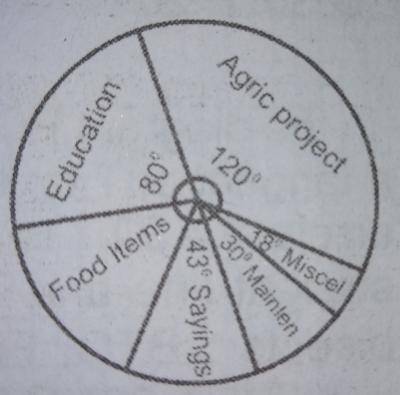

How much money did he invest in agriculture?
A.
N1,200.00
B.
N1,440.00
C.
N2,000.00
D.
N2,910.00
E.
N4,000.00
Correct answer is E
Agric project = 120360×N12,000.00
= N4,000.00
1,568.
The bearing of a point X from a point Y is 074°. What is the bearing of Y from X?
A.
106o
B.
146o
C.
164o
D.
254o
E.
286o
Correct answer is D
< YXS = 74° (alternate angles, N1 S1 // N2 S2)
N2 E2 S2 = 180°
∴ Bearing of Y from X = 180° + 74°
= 254°
1,569.
A.
3.6m
B.
3.8m
C.
6.0m
D.
9.3m
E.
26.1m
Correct answer is B
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests