2/3, 0, 6
3/2, 3, 6,
2/3, 3, 8/3
2/3, 3/4, 6
2/3, 3, 1/3
Correct answer is B
\(T_n = 3. 2^{n - 2} \)
\(T_{1} = 3. 2^{1 - 2} = 3. 2^{-1} \)
\(T_1 = \frac{3}{2} \)
\(T_2 = 3. 2^{2 - 2} \)
\(T_2 = 3. 2^0 = 3\)
\(T_3 = 3. 2^{3 - 2} = 3. 2^1 \)
\(T_3 = 6\)
The first 3 terms of the sequence are \(\frac{3}{2}\), 3 and 6.
3 9/17%
3 27/41%
15%
35 5/17%
36 24/41%
Correct answer is A
Error = 4.25 - 4.10 = 0.15
% error = \(\frac{0.15}{4.25} \times 100%\)
= \(\frac{15}{\frac{17}{4}} = \frac{15 \times 4}{17}\)
= \(3\frac{9}{17} %\)
Convert 77 to a number in base two
1001 101
111001
100110
10101
10011
Correct answer is A
\(\begin{array}{c|c} 2 & 77 \\ \hline 2 & 38 R1 \\ 2 & 19 R0 \\ 2 & 9 R1 \\ 2 & 4 R1 \\ 2 & 2 R0 \\ 2 & 1 R0 \\ & 0 R1\end{array}\)
77ten = 1001101two
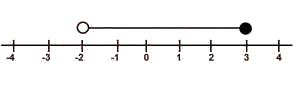
-3
-3≤x<2
-3
-3≤x≤2
x≥2
Correct answer is B
No explanation has been provided for this answer.
Simplify (3/4 + 1/3) x 4(1/3) ÷ 3(1/4)
1/2
13/12
10/9
17/12
13/9
Correct answer is E
(3/4 + 1/3) x 4(1/3) \(\div\) 3(1\4)
\(\begin{pmatrix} 9 + 4 \\ 12 \end{pmatrix}\) x \(\frac{13}{3}\) * \(\frac{4}{13}\)
= 9/4 or 1(4/9)
WAEC Subjects
Aptitude Tests