If \(y \propto \frac{1}{x^2}\) and x = 3 when y = 4, find y when x = 2.
1
3
9
18
21
Correct answer is C
\(y \propto \frac{1}{x^2}\)
\(y = \frac{k}{x^2}\)
\(4 = \frac{k}{3^2}\)
\(k = 4 \times 3^2 = 36\)
\(y = \frac{36}{x^2}\)
When x = 2,
\(y = \frac{36}{2^2} = 9\)
Factorize the expression x(a - c) + y(c - a)
(a - c)(y - x)
(a - c)(x - y)
(a + c)(x - y)
(a + c)(x + y)
(a - c)(x + y)
Correct answer is B
x(a - c) + y(c - a)
= x(a - c) - y(a - c)
= (x - y)(a - c)
What is the smaller value of x for which x\(^2\) - 3x + 2= 0?
1
2
3
4
5
Correct answer is A
x\(^2\) - 3x + 2 = 0
x\(^2\) - 2x - x + 2 = 0
x(x - 2) - 1(x - 2) = 0
(x - 2)(x - 1) = 0
x = 1 or 2. The smaller value of x = 1.
Solve the inequality: \(\frac{1}{3}(2x - 1) < 5\)
x < - 5
X<-6
X<7
x <8
x < 16
Correct answer is D
\(\frac{1}{3}(2x - 1) < 5\)
\(2x - 1 < 15\)
\(2x < 16\)
\(x < 8\)
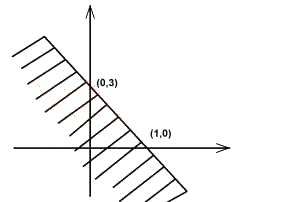
Which of the following could be the inequality illustrated in the sketch graph above?
y≥2x+3
y≤-3x+3
y < 3x+2
y≤x +3
y≥3x+2.
Correct answer is B
Gradient of the line = \(\frac{3 - 0}{0 - 1}\)
= -3
y = -3x + b.
Using (1,0), we have
0 = -3(1) + b
0 = -3 + b
b = 3
y = -3x + 3
\(\therefore\) The graph illustrates y \(\leq\) -3x + 3.
WAEC Subjects
Aptitude Tests