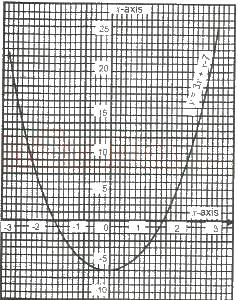
1.0 And -1.2
1.1and-1.3
1.4and-1.7
2.0 and -1.9
2.4 and -2.0
Correct answer is C
No explanation has been provided for this answer.
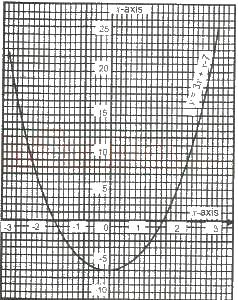
Use the graph of y = 3x\(^2\) + x - 7 above to answer the question What is the minimum value of y?
-10
-7
-4
-1
2
Correct answer is B
No explanation has been provided for this answer.
-2
-1
1/2
1
31/2
Correct answer is D
x + y = \(\frac{3}{2}\) ... (i)
x - y = \(\frac{5}{2}\) ... (ii)
(i) - (ii):
2y = \(\frac{-2}{2}\) = -1
y = \(-\frac{1}{2}\)
x + y = \(\frac{3}{2}\)
x - \(\frac{1}{2}\) = \(\frac{3}{2}\)
x = \(\frac{3}{2} + \frac{1}{2}\)
= \(\frac{4}{2}\)
x = 2
\(\therefore\) 2y + x = 2(\(-\frac{1}{2}\)) + 2
= -1 + 2 = 1.
Solve the equation (x +2)(x - 7) = 0
x = 1 or 8
x = -2 or 7
x = -4 or 5
x = -3 or 6
x= -5 or -2
Correct answer is B
(x + 2)(x - 7) = 0 x + 2 = 0 ⟹ x = -2 x - 7 = 0 ⟹ x = 7 x = -2 or 7
Solve the equation 3x\(^2\) + 25x -18 = 0
-3,2
-2,3
-2,9
-9,2/3
2/3, 9.
Correct answer is D
3x\(^2\) + 25x - 18 = 0
3x\(^2\) + 27x - 2x - 18 = 0
3x(x + 9) - 2(x + 9) = 0
(3x - 2)(x + 9) = 0
x = \(\frac{2}{3}\) or x = -9.
WAEC Subjects
Aptitude Tests