132.
If 16 * 2(x+1) = 4x * 8(1−x), find the value of x.
A.
-4
B.
4
C.
1
D.
-1
Correct answer is D
16 * 2(x+1) = 4x * 8(1−x)
= 24 * 2(x+1) = 22x * 23(1−x)
--> 4 + x + 1 = 2x + 3 - 3x
collect like terms
--> x - 2x + 3x = 3 - 1 - 4
--> 2x = -2
--> x = -1
133.
if p = {-3<x<1} and Q = {-1<x<3}, where x is a real number, find P n Q.
A.
0
B.
-3, -2, -1, 0 and 1
C.
-2, -1 and 0
D.
-1, 0 and 1
Correct answer is A
p = {-3<x<1} = {-2,-1 and 0}
Q = {-1<x<3} = {0,1 and 2}
P n Q = {0} or {-1<x<1}
134.
Find the least value of x which satisfies the equation 4x = 7(mod 9)
A.
7
B.
6
C.
5
D.
4
Correct answer is D
4x = 7 (mod 9)
4x = 7 + 9 (mod 9)
4x4=164 (mod 9)
x = 4
135.
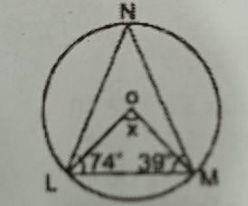

A.
134o
B.
126o
C.
113o
D.
106o
Correct answer is A
LNM = 180o - (74o + 39o)
180o - 113o
= 67o
LO
M = x = 2 x 67o
= 134o
WAEC Subjects
Aptitude Tests