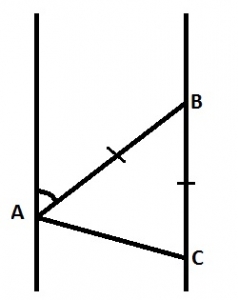
\frac{x}{sin 40^o}
\frac{x}{cos 40^o}
\frac{x}{2 sin 40^o}
\frac{x}{2 cos 40^o}
Correct answer is C
No explanation has been provided for this answer.
If tan x = \frac{1}{\sqrt{3}}, find cos x - sin x such that 0^o \leq x \leq 90^o<
\frac{\sqrt{3}+1}{2}
\frac{2}{\sqrt{3}+1}
\frac{\sqrt{3}-1}{2}
\frac{2}{\sqrt{3}-1}
Correct answer is C
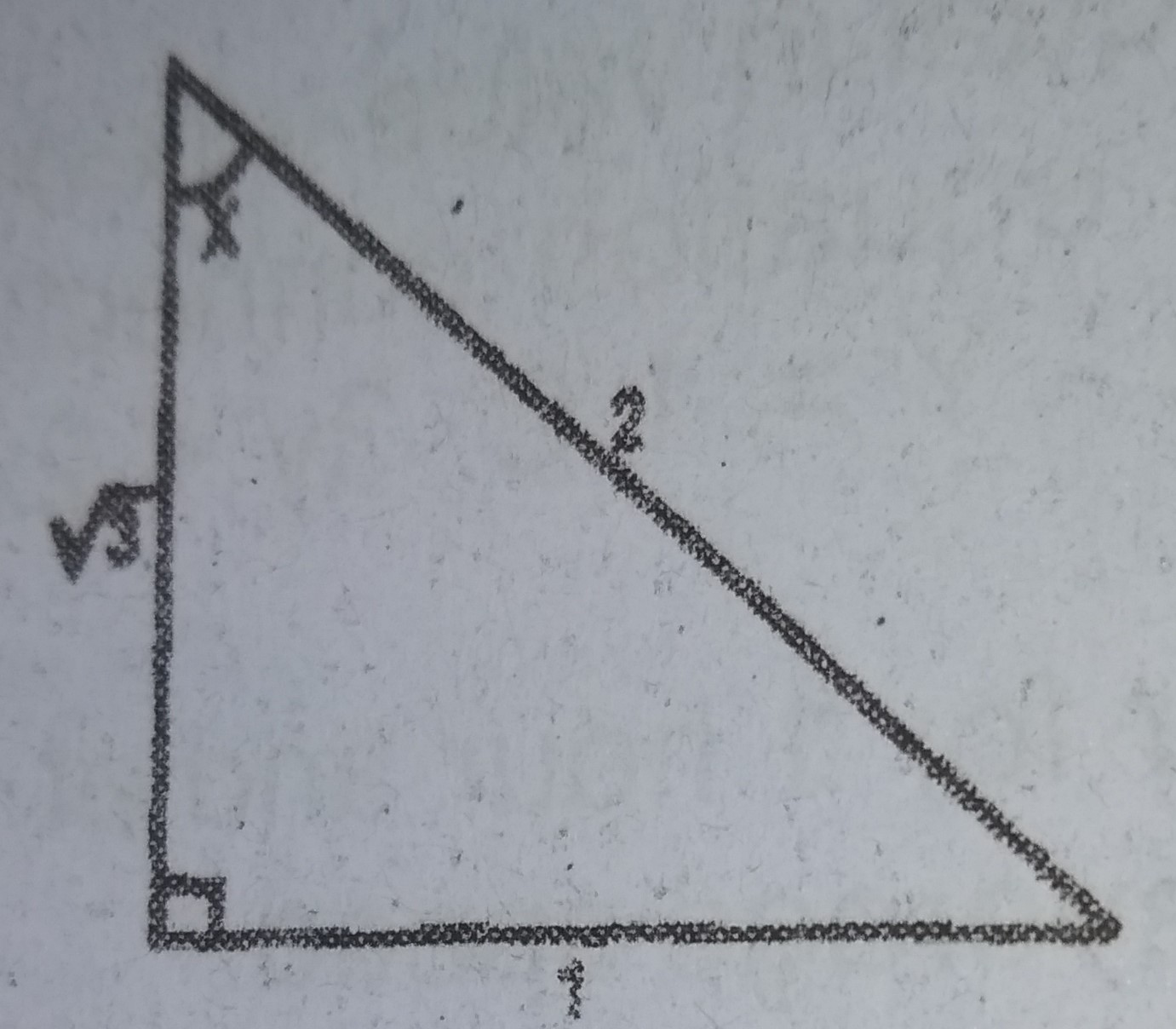
\cos x = \frac{\sqrt{3}}{2}
\sin x = \frac{1}{2}
\cos x - \sin x = \frac{\sqrt{3} - 1}{2}
If y varies inversely as x^2, how does x vary with y?
x varies inversely as y2
x varies inversely as √y
x varies directly as y2
x varies directly as
Correct answer is B
y \propto \frac{1}{x^2}
y = \frac{k}{x^2}
x^2 = \frac{k}{y}
x = \frac{\sqrt{k}}{\sqrt{y}}
Since k is a constant, then \sqrt{k} is also a constant.
\therefore x \propto \frac{1}{\sqrt{y}}
WAEC Subjects
Aptitude Tests