Solve the inequality 2x + 3 < 5x
\(x>1\)
\(x<\frac{3}{7}\)
\(x>\frac{3}{7}\)
\(x>-1\)
Correct answer is A
2x + 3 < 5x
-3x < -3
X > 1
\(\frac{7}{25}\)
\(\frac{41}{50}\)
\(\frac{1}{2}\)
1
Correct answer is A
P(man picked at random wears size 9 shoes) = \(\frac{28}{100}\)
= \(\frac{7}{25}\)
The root of a quadratic equation in x, are -m and 2n. Find the equation
\(x^2 + x(m - 2n)-2mn=0\)
\(x^2 - x(m - 2n)-2mn=0\)
\(x^2 - x(m - 2n)+2mn=0\)
\(x^2 + x(m - 2n)+2mn=0\)
Correct answer is A
x = -m \(\implies\) x + m = 0;
x = 2n \(\implies\) x - 2n = 0.
\(\implies (x + m)(x - 2n) = 0\)
\(x^2 + mx - 2nx - 2mn = 0\)
\(x^2 + x(m - 2n) - 2mn = 0\)
If \(x^2 +15x + 50 = ax^2 + bx + c = 0\). Which of the following statement is not true?
x = -5
x = 10
x + 10 = 0
bc = 750
Correct answer is B
\(x^2 + 15x + 50 = 0\)
\(x^2 + 5x + 10x + 50 = 0\)
\(x(x + 5) + 10(x + 5) = 0\)
\((x + 5)(x + 10) = 0\)
x + 5 = 0 or x + 10 = 0.
Comparing \(x^2 + 15x + 50\) with \(ax^2 + bx + c\), b = 15 and c = 50.
\(\therefore\) bc = 750.
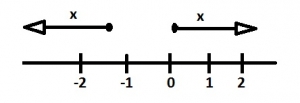
Which of the following pairs of inequalities is represented on the number line?
\(x<-2 and x\ge1\)
\(x\ge -2 and x>1\)
\(x\le -2 and x\ge1\)
\(x< -2 and x>1\)
Correct answer is C
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests