1,141.
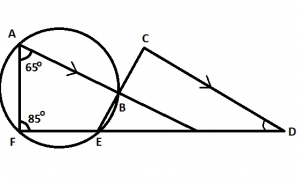

A.
20o
B.
30o
C.
50o
D.
65o
Correct answer is B
No explanation has been provided for this answer.
1,142.
A.
16
B.
17
C.
34
D.
90
Correct answer is B
82+(x−2)2=x264+x2−4x+4=x2x2−4x+68=x2−4x=−68−x=−684=17
1,143.
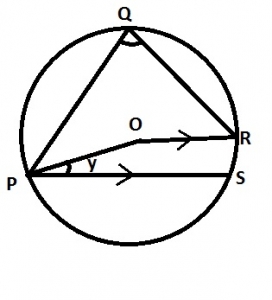

A.
15
B.
30
C.
45
D.
75
Correct answer is B
No explanation has been provided for this answer.
1,144.
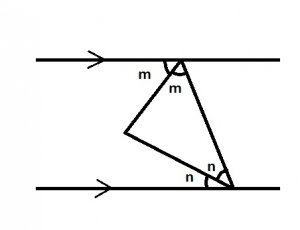

Which of the following statements is true from the diagram above?
A.
m + n = 90o
B.
m = n
C.
n > 45o
D.
m < 45o
Correct answer is A
No explanation has been provided for this answer.
1,145.
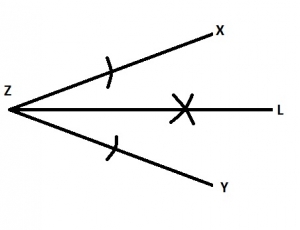

Describe the locus L shown in the diagram below
A.
Locus of points equidistant from X and Y
B.
Locus of points equidistant from X and Z
C.
Locus of points equidistant from ¯ZX and ¯ZY
D.
Locus of points equidistant from ¯XY and ¯ZY
Correct answer is C
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests