If the interior angles of hexagon are 107°, 2x°, 150°, 95°, (2x-15)° and 123°, find x.
5712∘
65∘
106∘
120∘
Correct answer is B
Sum of interior angle in a hexagon = (6 - 2) x 180°
= 720°
∴ 107° + 2x° + 150° + 95° + (2x - 15)° + 123° = 720°
460 + 4x = 720 \implies 4x = 720 - 460
4x = 260° \implies x = 65°
75o
150o
160o
68o
Correct answer is B
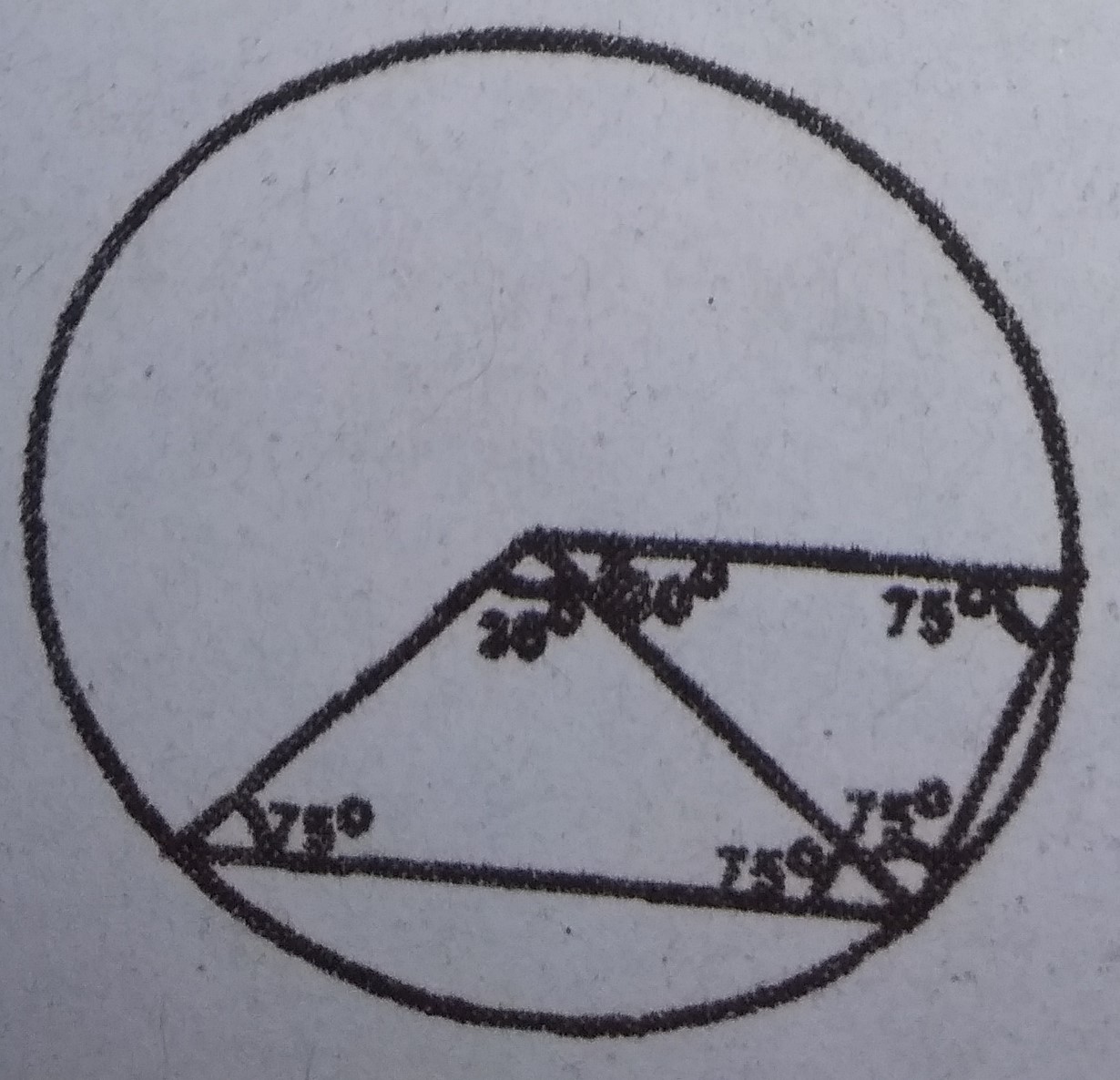
Interior angle = 2(75°)
= 150°
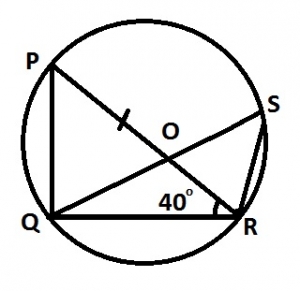
In the diagram, PQRS is a circle center O. PQR is a diameter and ∠PRQ = 40°. Calculate ∠QSR
30o
40o
45o
50o
Correct answer is D
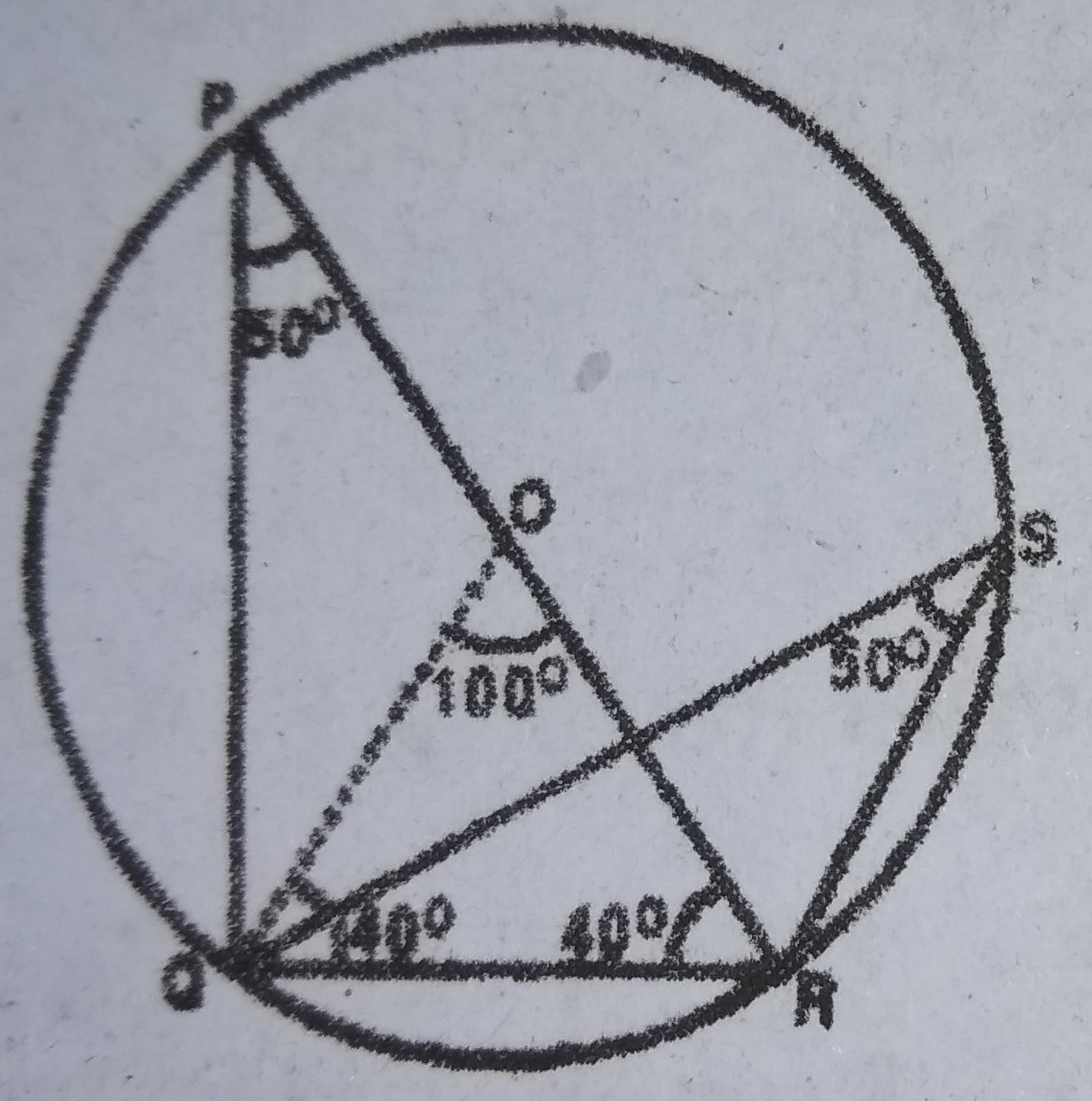
< Q = < R (OQ = OR = radii)
< QOR = 180° - 2(40°) = 100°
< QSR = < RPQ = \frac{1}{2} < QOR
= \frac{100}{2} = 50°
Which of the following statement is not true about a rectangle?
I.Each diagonal cuts the rectangle into two congruent triangles.
II. A rectangle has four lines of symmetry
III. The diagonals intersect at right angles
I and II only
III only
II only
II and III only
Correct answer is B
No explanation has been provided for this answer.
\frac{1}{10}
\frac{3}{10}
\frac{9}{20}
\frac{2}{3}
Correct answer is A
P(Kodjo passing) = \frac{3}{4}; P(Adoga passing) = \frac{3}{5}
P(Kodjo failing) = \frac{1}{4}; P(Adoga failing) = \frac{2}{5}
P(both fail) = \frac{1}{4} \times \frac{2}{5}
= \frac{1}{10}
WAEC Subjects
Aptitude Tests