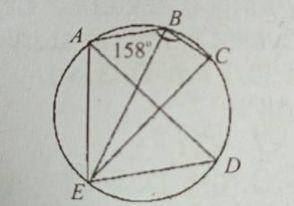
In the diagram, line ¯EC is a diameter of the circle ABCDE.
If angle ABC equals 158°, find ∠ADE
112
90
68
22
Correct answer is C
No explanation has been provided for this answer.
Given that sin x = 3/5, 0 ≤ x ≤ 90, evaluate (tanx + 2cosx)
21120
1120
2720
120
Correct answer is B
Sin x = opphyp
sinx = 35
using Pythagoras' theorem
hyp2 = opp2 + adj2
adj2 = 52 - 32 = 25 - 9
adj2 = 16
adj = √ 16
adj = 4.
tanx = oppadj
= 34
cosx = adjhyp
= 45
(tanx + 2cosx) = 34 + 2(45)
= 15+3220
= 4720 or
2 720
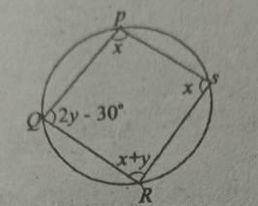
In the diagram, PQRS is a circle. find the value of x.
50°
30°
80°
100°
Correct answer is A
Opp. angles in a cyclic quadrilateral always add up to 180°
∠P + ∠R & ∠Q + ∠S = 180
x + x+y = 180
2x + y = 180... i
2y - 30 + x = 180
2y + x = 180 + 30
x + 2y = 210 ... ii
Elimination method:
(2x + y = 180) * 1 --> 2x + y = 180
(x + 2y = 210) * 2 --> 2x + 4y = 420
Subtracting both equations
- 3y = - 240
y = 80°
using eqn i
2x + y = 180
2x + 80 = 180
2x = 100
x = 50°
find the first quartile of 7,8,7,9,11,8,7,9,6 and 8.
8.5
7.0
7.5
8.0
Correct answer is B
Rearrange data in increasing order: 6,7,7,7,8,8,8,9,9 and 11
First quartile (ungrouped data) = n4th value
= 104
= 2.5th value
= 7+72
= 7.0
WAEC Subjects
Aptitude Tests