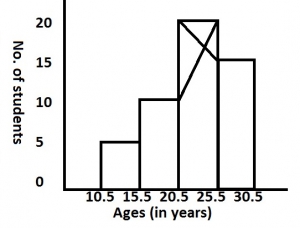
22.5 years
23.0 years
24.0 years
27.5 years
Correct answer is B
No explanation has been provided for this answer.
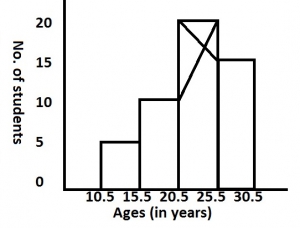
What is the range of their age?
14 years
20 years
30.5 years
31 years
Correct answer is B
Range = 30.5 - 10.5
= 20 years
p-q=1
q-p=0
p+q=1
p+q=0
Correct answer is C
No explanation has been provided for this answer.
\(\frac{2}{11}\)
\(\frac{5}{12}\)
\(\frac{8}{12}\)
\(\frac{7}{11}\)
Correct answer is A
Total number of balls = 5 + 3 + 4 = 12 balls
P(one ball is green and the other is blue) = P(first ball is green and second blue) + P(first ball is blue and the second green)
= \(\frac{3}{12} \times \frac{4}{11} + \frac{4}{12} \times \frac{3}{11}\)
= \(\frac{2}{11}\)
\(\frac{5}{33}\)
\(\frac{5}{36}\)
\(\frac{103}{132}\)
\(\frac{31}{36}\)
Correct answer is A
Total number of balls = 5 + 3 + 4
= 12 balls
P(first ball is red) = \(\frac{5}{12}\)
P(second ball is red) = \(\frac{4}{11}\)
\(\therefore\) P(both balls are red) = \(\frac{5}{12} \times \frac{4}{11}\)
= \(\frac{5}{33}\)
WAEC Subjects
Aptitude Tests