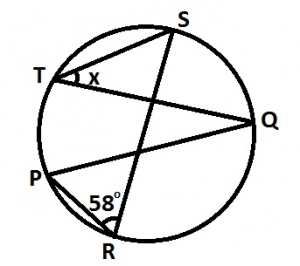
In the diagram, PQ is the diameter of the circle and ∠PRS = 58°. Find ∠STQ.
29o
32o
42o
53o
Correct answer is B
In Δ PRQ, < SRQ = 90° - 58°
< SRQ = < QTS = x (angles in the segment)
∴ x = 32°
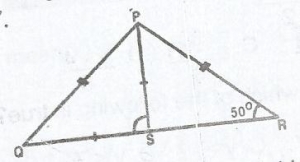
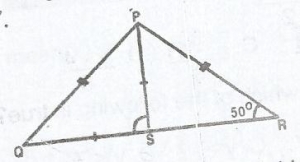
In the diagram, PQR is a triangle.|PQ| = |PR|, |PS| = |SQ| and PRS = 50°. What is the size of ∠PSQ?
75o
80o
85o
95o
Correct answer is B
< PQS = 50° (PQ = PR)
< PQS = < SPQ = 50° (QS = PS)
In triangle PSQ, < PQS + < QPS + < PSQ = 180°
50° + 50° + < PSQ = 180°
< PSQ = 180° - 100° = 80°
Which of the following is not the the size of an exterior angle of a regular polygon?
15o
18o
20o
21o
Correct answer is D
The size of an exterior angle = \frac{360}{n}
From the options, all options can perfectly divide 360°, except 21°.
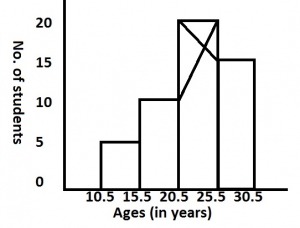
How many students are there in the group?
25
30
52
55
Correct answer is C
Total number of students = 20 + 16 + 10 + 6
= 52 students
WAEC Subjects
Aptitude Tests