Find the value of x in 0.5x + 2.6 = 5x + 0.35
0.5
2
2.6
5
Correct answer is A
\(0.5x + 2.6 = 5x + 0.35\\
0.5x - 5x = 0.35-2.6\\
-4.5x = -2.25\\
x = \frac{-2.25}{-4.5}\\
0.5\)
{a,c}
{a, c, d, g}
{c, d, g}
{a, c, g}
Correct answer is D
U = {a, b, c, d, e, f, g} P = {b, d, e, f} Q = {a, c, f, g} P' = {a, c, g} P' ∩ Q = {a, c, g}
The variance of a given distribution is 25. What is the standard deviation?
125
75
25
5
Correct answer is D
S.D = \(\sqrt{Variance}\)
= \(\sqrt{25}\)
= 5
Simplify \(5\frac{1}{4}\div \left(1\frac{2}{3}- \frac{1}{2}\right)\)
\(1\frac{3}{4}\)
\(3\frac{1}{2}\)
\(4\frac{1}{2}\)
\(8\frac{1}{2}\)
Correct answer is C
\(5\frac{1}{4}\div \left(1\frac{2}{3}- \frac{1}{2}\right)\\
\frac{21}{4}\div \left(1\frac{4-3}{6}\right)\\
\frac{21}{4}\div \left(1\frac{1}{6}\right)\\
\frac{21}{4} \times \frac{6}{7}= 4\frac{1}{2}\)
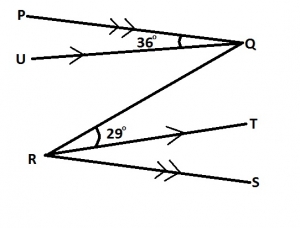
In the diagram above, ∠PQU=36°, ∠QRT = 29°, PQ||RT. Find ∠PQR
94o
65o
61o
54o
Correct answer is B
< UQR = 29° (alternate angles)
< PQR = < PQU + < UQR
= 36° + 29°
= 65°
WAEC Subjects
Aptitude Tests