Simplify \(\frac{2^{\frac{1}{2}}\times 8^{\frac{1}{2}}}{4}\)
1
2
4
16
Correct answer is A
\(\frac{2^{\frac{1}{2}}\times 8^{\frac{1}{2}}}{4}\\=\frac{2^{\frac{1}{2}}\times 2^{\frac{3}{2}}}{2^2}\\=2^{\frac{1}{2}}+2^{\frac{3}{2}}-2=2^0 = 1\)
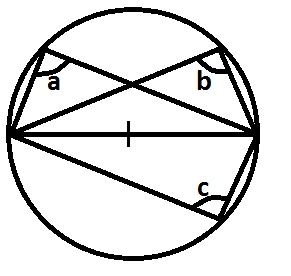
I and II only
II and III only
II only
III only
Correct answer is A
No explanation has been provided for this answer.
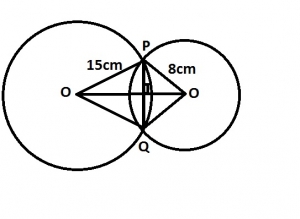
8.46cm
19.04cm
20.81cm
26.16cm
Correct answer is B
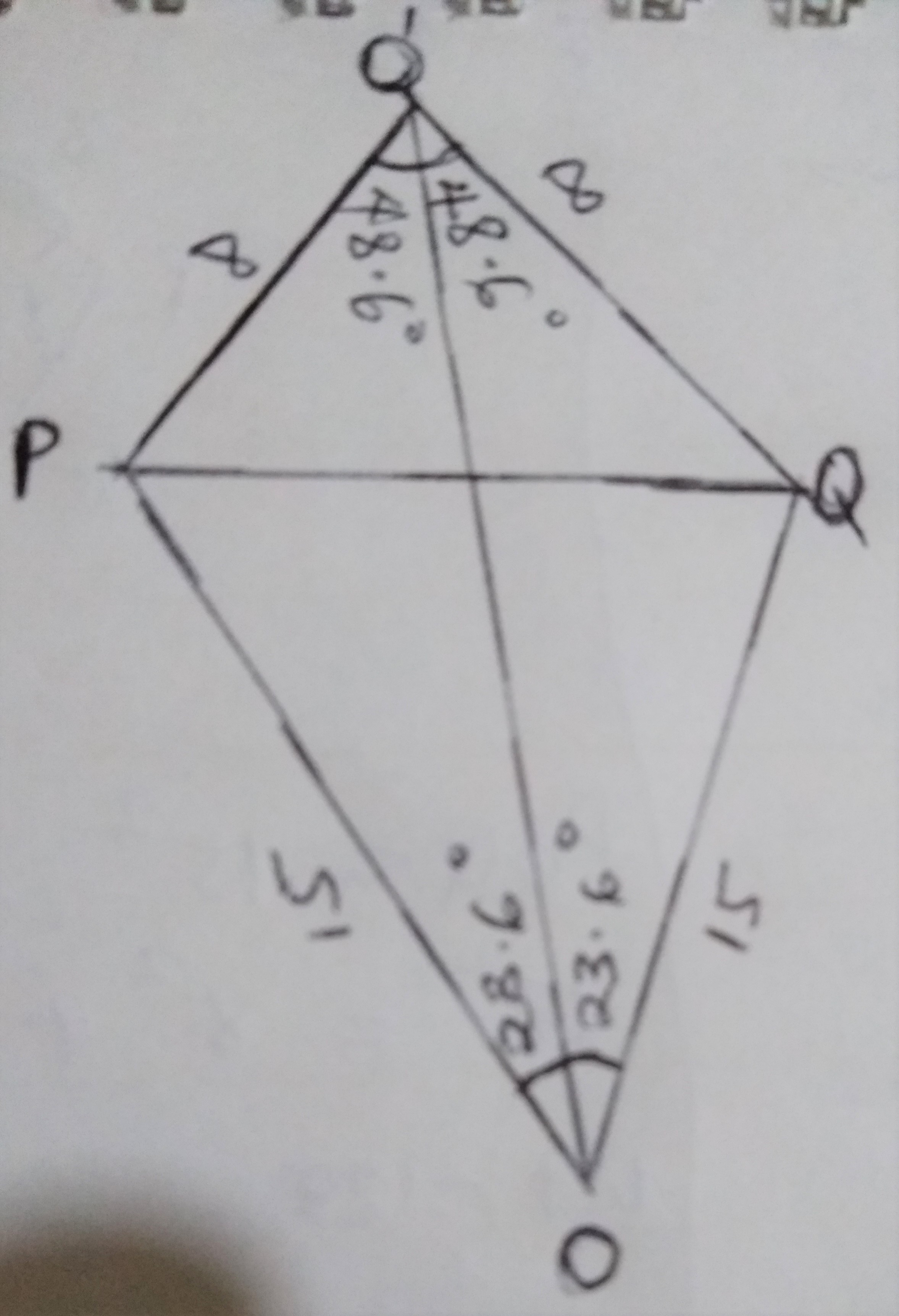
In \(\Delta\) POQ,
\(12^2 = 15^2 + 15^2 - 2(15)(15) \cos < POQ\)
\(144 = 450 - 450\cos < POQ\)
\(450 \cos < POQ = 450 - 144 = 306\)
\(\cos <POQ = \frac{306}{450} = 0.68\)
\(< POQ = 47.2°\)
In \(\Delta\) PO'Q,
\(12^2 = 8^2 + 8^2 - 2(8)(8) \cos <PO'Q\)
\(144 - 128 = -128 \cos < PO'Q\)
\(\cos < PO'Q = - 0.125\)
\(< PO'Q = 97.2°\)
In \(\Delta\) POQ,
\(\cos 23.6 = \frac{x}{15}\)
\(x = 15 \times \cos 23.6\)
= 13.75 cm
In \(\Delta\) PO'Q,
\(\cos 48.6 = \frac{y}{8}\)
\(y = 8 \times \cos 48.6\)
= 5.29 cm
\(\therefore\) OO' = x + y = 13.75 + 5.29
= 19.04 cm
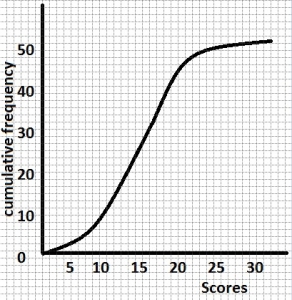
The upper quartile of the distribution is
30
27.5
25
17.75
Correct answer is D
No explanation has been provided for this answer.
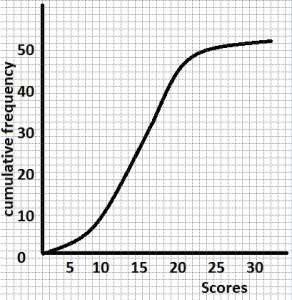
The range of the distribution is
50
30
25
15
Correct answer is C
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests