Simplify \(\frac{4\sqrt{18}}{\sqrt{8}}\)
2
3
6
12
Correct answer is C
\(\frac{4\sqrt{18}}{\sqrt{8}}\\
= \frac{4\sqrt{9\times 2}}{\sqrt{4 \times 2}} = \frac{12\sqrt{2}}{2\sqrt{2}}=\frac{6\sqrt{2}}{\sqrt{2}}\\
Rationalising \frac{6\sqrt{2}}{\sqrt{2}}\\
=\frac{6\sqrt{2}}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = 6\)
N5.00
N7.50
N10.00
N15.00
Correct answer is A
Represent notebook with x
Represent pen with y
∴ 3x+y=35 ---- (i)
2x+2y=30 ---- (ii)
Multiply eqn (i) by 2 and eqn (ii) by 1
6x+2y=70 ---- (iii)
2x+2y=30 ---- (iv)
Subtract eqn (iv) from eqn (iii)
4x = 40
X = 10
Substitute x = 10 in eqn (i)
3x+y=35
3(10)+y=35
Y = 5
∴ The cost of pen is N5.00
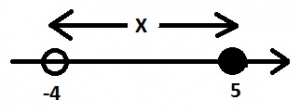
Interprete the inequality represented on the number line
-4< X ≤ 5
-4 ≤ x< 5
-4
-4≤x≤5
Correct answer is A
No explanation has been provided for this answer.
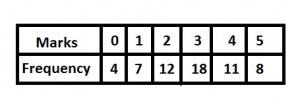
12
23
37
49
Correct answer is D
= 12 + 18 + 11 + 8
= 49 students
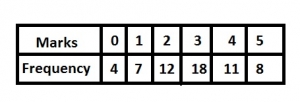
1
2
3
4
Correct answer is C
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests