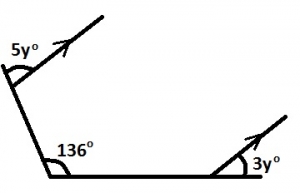
Calculate the value of y in the diagram
17
34
44
45
Correct answer is A
Sum of interior angle of the diagram equals 360o
180o - 5yo + 136o + 180o + 180o - 3yo = 360o
-8yo + 136o = 0
-8yo = -136; y = 17
60
80
100
360
Correct answer is B
Sum of interior angles in a quadrilateral is 360
(x + 20)o + (x+ 10)o + (2x - 45)o + (x - 25)o = 360o
5xo - 40o = 360o
x = 400/5 = 80o
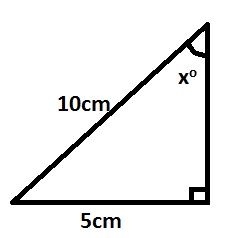
What is the size of angle x in the diagram
15o
30o
45o
60o
Correct answer is B
\(Sin\theta^{\circ} = \frac{opp}{hyp}\\
Sin X^{\circ}=\frac{5}{10}=0.5000\\SinX^{\circ}\\
X^{\circ} = sin^{-1}0.5000\\
X^{\circ}=30^{\circ}\)
3.611m
4.521m
4.792m
7.962m
Correct answer is C
Sin 53 = \(\frac {h}{6} \)
h = 6 sin 53 = 6 x 0.7986
= 4.792m
Given, that \(4P4_5 = 119_{10}\), find the value of P
1
2
3
4
Correct answer is C
\(4P4_5 = 119_{10}\)
\(4 \times 5^2 + P \times 5^1 + 4 \times 5^0 = 119\)
\(100 + 5P + 4 = 119\)
\(5P = 119 - 104 = 15\)
\(P = 3\)
WAEC Subjects
Aptitude Tests