A right circular cone is such that its radius r is twice its height h. Find its volume in terms of h
\(\frac{2}{3}\pi h^2\)
\(\frac{1}{12}\pi h^3\)
\(\frac{4}{3}\pi h^2\)
\(\frac{4}{3}\pi h^3\)
Correct answer is D
Volume of a cone = \(\frac{\pi r^2 h}{3}\)
r = 2h.
V = \(\frac{\pi \times (2h)^2 \times h}{3}\)
= \(\frac{4}{3} \pi h^3\)
55cm2
25cm2
22cm2
13cm2
Correct answer is A
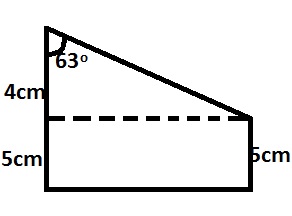
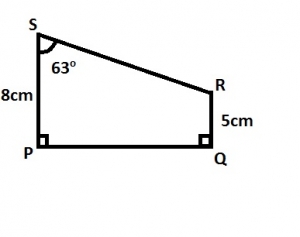
Considering the triangle in the diagram
\(tan\theta = \frac{opp}{hyp}\\
Tan 63^{\circ} = \frac{h}{4}\\
h = 4 tan 63^{\circ}\\
Area of trapezium = \frac{1}{2}h(a+b)\\
\left(\frac{1}{2} \times 4 tan 63^{\circ}[5+9]\right)\\
=28\times 1.963 = 54.96 = 55cm^2\)
90o
75o
60o
45o
Correct answer is C
No explanation has been provided for this answer.
Evaluate Cos 45o Cos 30o - Sin 45o Sin 30o leaving the answer in surd form
\(\frac{\sqrt{2}-1}{2}\)
\(\frac{\sqrt{3}-\sqrt{2}}{4}\)
\(\frac{\sqrt{6}-\sqrt{2}}{2}\)
\(\frac{\sqrt{6}-\sqrt{2}}{4}\)
Correct answer is D
\(cos45^o \times cos30^o - sin45^o \times sin30^o\\
\frac{1}{\sqrt{2}}\times \frac{\sqrt{3}}{2} - \frac{1}{\sqrt{2}}\times \frac{1}{2}\\
\frac{\sqrt{3}}{2\sqrt{2}}-\frac{1}{2\sqrt{2}}; = \frac{\sqrt{3}-1}{2\sqrt{2}}=\frac{\sqrt{6}-\sqrt{2}}{4}\)
Find the equation whose roots are \(-\frac{2}{3}\) and 3
3x2+11x-6=0
3x2+7x+6=0
3x2-11x-6=0
3x2-7x-6=0
Correct answer is D
\(x = -\frac{2}{3} \implies x + \frac{2}{3} = 0\)
\(x = 3 \implies x - 3 = 0\)
\(\implies (x - 3)(x + \frac{2}{3}) = 0\)
\(x^2 - 3x + \frac{2}{3}x - 2 = 0\)
\(x^2 - \frac{7}{3}x - 2 = 0\)
\(3x^2 - 7x - 6 = 0\)
WAEC Subjects
Aptitude Tests