33
8
7
0
Correct answer is C
\(7\frac{1}{2}-\left(2\frac{1}{2}+3\right)\div16\frac{1}{2}\); \(\frac{15}{2} - \left(\frac{5}{2}+\frac{3}{1}\right)\div \frac{33}{2}\)
\(\frac{15}{2} - \left(\frac{5+6}{2}\right)\div \frac{33}{2}\); \(\frac{15}{2} - \frac{11}{2} \div \frac{33}{2}\)
\(\frac{11}{2}\) ÷ \(\frac{33}{2}\) = \(\frac{11}{2}\) * \(\frac{2}{33}\)
= \(\frac{11}{33}\) or \(\frac{1}{3}\) (when simplified)
\(\frac{15}{2}\) - \(\frac{1}{3}\) = \(\frac{43}{6}\)
7.166
The nearest whole number is 7
\(\frac{m}{12}\)
\(\frac{12}{m}\)
\(\frac{12}{m+12}\)
\(\frac{12}{m-12}\)
Correct answer is C
Prob. (a girl) \(=\frac{Number\hspace{1mm} of\hspace{1mm} girls}{Number \hspace{1mm} of \hspace{1mm} boys \hspace{1mm} and \hspace{1mm} girls\hspace{1mm} in \hspace{1mm} class}\\
= \frac{12}{m+12}\)
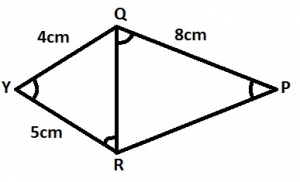
2.0cm
2.5cm
6.4cm
10.0cm
Correct answer is C
\(\frac{PR}{QR} = \frac{QR}{QY} = \frac{QP}{YR}\) (SSS Congruence)
\(\frac{QR}{4} = \frac{8}{5}\)
\(QR = \frac{4 \times 8}{5}\)
= 6.4 cm
\(\frac{5}{6}\)
\(\frac{7}{12}\)
\(\frac{5}{12}\)
\(\frac{1}{6}\)
Correct answer is C
Let the girls pocket money be rep. by x. The amount spent on books = \(\frac{1}{4}of\hspace{1mm}x = \frac{x}{4}\)
The amount spent on dress \(=\frac{1}{3} of \hspace{1mm}x=\frac{x}{3}\)
∴The fraction that remains = \(\frac{x}{1}-\left(\frac{x}{4}+\frac{x}{3}\right)\\
\frac{3x+4x}{12}; = \frac{12x-7x}{12} = \frac{5x}{12} = \frac{5}{12}\)
Solve for t in the equation \(\frac{3}{4}t+\frac{1}{3}(21-t)\) = 11,
\(\frac{9}{13}\)
\(\frac{9}{5}\)
5
\(9\frac{3}{5}\)
Correct answer is D
\(\frac{3}{4}t+\frac{1}{3}(21-t) = 11; \frac{3t}{4} + \frac{7}{1} - \frac{t}{3} = \frac{11}{1}\\
\frac{3 \times 3t + 7\times 12 – 4 \times t = 11 \times 12}{12}\\
9t + 84 – 4t = 132; 5t = 132 – 84\\
5t = 48; t = \frac{48}{5} = 9\frac{3}{5}\)
WAEC Subjects
Aptitude Tests