What is the volume of a solid cylinder of diameter 7cm and height 7cm? (Take π=227)
38.5cm3
77cm3
269.5cm3
1078cm3
Correct answer is C
Volume of a solid cylinder = Base area x height
Base area =πr2=227×72×72=772
Volume of a solid cylinder = 772×71=5392cm3=269.5cm3
9(3px - 4y)2
3(3px - 4y)(3px - 4y)
9(px - 4y)(3p x + 4y)
3(3px -4y)(3px +4y)
Correct answer is D
27p2x2 - 48y2; 3(32 p2x2-42y2)
3[(3px) 2 - (4y) 2]; 3[(3px-4y)(3px+4y)]
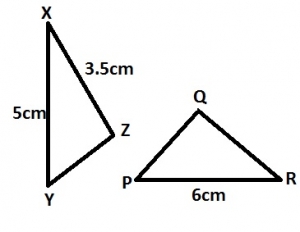
In the diagram, ∆XYZ is similar to ∆PRQ, |XY| = 5cm, |XZ| =3.5cm and |PR| = 8cm. Find |PQ|
5.6 cm
11.2cm
11.4cm
28.0cm
Correct answer is A
PQPR=XZXY;PQ8=3.55PQ=8×3.55=285=5.6cm
Find, correct to two decimal places, the mean of 9, 13, 16, 17, 19, 23, 24.
23.00
17.29
16.50
16.33
Correct answer is B
Mean =sumofallthenumbersTotalNumber9+13+16+17+19+23+2471217=17.2857=17.29
Solve the equation 10-3x-x2 = 0
x=2 or-5
x= -2 or 5
x = 1 or 10
x = 2 or 5
Correct answer is A
10 – 3x - x2 = 0; 10 – 5x + 2x - x2 = 0
5(2 – x) + x(2 – x) = 0; (2 – x)(5 + x) = 0
2 – x = 0 or 5 + x = 0; x = 2 or x = -5
WAEC Subjects
Aptitude Tests