Processing math: 100%

WAEC Mathematics Past Questions & Answers - Page 180

896.

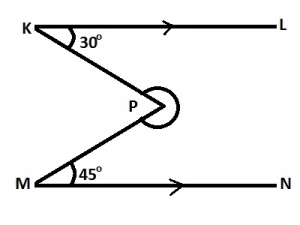
In the diagram, KL//MN, ∠LKP = 30^o and ∠NMP = 45^o. Find the size of the reflex ∠KPM.

285^o

255^o

225^o

210^o

View answer & explanation

Correct answer is A

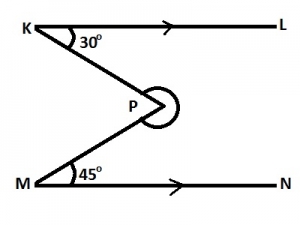
∠KPM = 360^o - (30 + 45)^o
= 360^o - 75^o = 285^o

897.

A fair die is tossed once, what is the probability of obtaining neither 5 or 2

$\frac{5}{6}$

$\frac{2}{3}$

$\frac{1}{2}$

$\frac{1}{6}$

View answer & explanation

Correct answer is B

Probability of obtaining a 5 is P(5)= $\frac{1}{6}$
Probability of obtaining a 2 is P(2)= $\frac{1}{6}$
Probability of obatining either 2 or 5 = P(2∪5) = $\frac{2}{6}$
Probability of obtaining neither 5 or 2 = $1 - \frac{2}{6}=\frac{4}{6}=\frac{2}{3}$

898.

From a point P, R is 5km due west and 12km due south. Find the distance between P and R

5km

12km

13km

17km

View answer & explanation

Correct answer is C

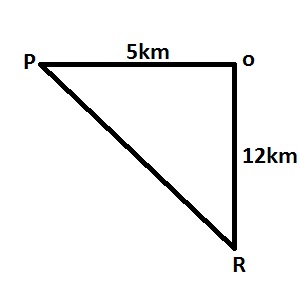
Using Pythagoras theorem
$|PR|^2=|PO|^2+|OR|^2\\ |PR|^2=5^2+12^2\\ |PR|=\sqrt{25+144}=\sqrt{169}=13km$

899.

A man bought 220 mangoes at N5x. He sold each for 3x kobo and made a gain of N8. Find the value of x

View answer & explanation

Correct answer is B

The cost price of the whole mangoes = N5x
The sold amount of the mangoes = 3x * 220 = N6.60x
The gain made on mangoes = N6.60x - N5x = N8.00 => N1.60x = N8 => $x=\frac{8}{1.60}=\frac{1}{0.2}=\frac{10}{2}=5$

900.

Find the equation whose roots are 2 and $-3\frac{1}{2}$

2x² + 3x + 14 = 0

2x² + 5x + 7 = 0

2x² + 5x - 7 = 0

2x² + 3x - 14 = 0

View answer & explanation

Correct answer is D

x² (sum of roots)x + (product of roots) = 0
Sum of roots $2+-3\frac{1}{2} = -1\frac{1}{2}=-\frac{1}{2}$
Product of roots $=2 \times -3\frac{1}{2}=-7\\ x^2-\left(\frac{-3}{2}\right)x+(-7)=0\Rightarrow 2x^2 + 3x - 14 = 0$