Processing math: 100%

WAEC Mathematics Past Questions & Answers - Page 178

886.

From a point R, 300m north of P, man walks eastward to a place Q which is 600m from P. Find the bearing of P from Q, correct to the nearest degree

026^o

045^o

210^o

240^o

View answer & explanation

Correct answer is D

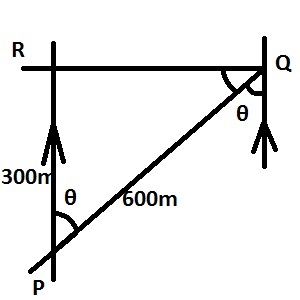
$cos\theta = \frac{adj}{hyp}=\frac{300}{600}=\frac{1}{2}\\ \theta = cos^{-1}(0.5000)=60^{\circ}$
The bearing of P from $Q = \theta + 180 = 60 + 180 = 240^{\circ}$

887.

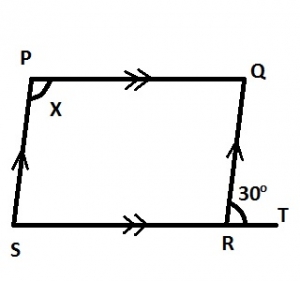
In the diagram, PQRS is a parallelogram and ∠QRT = 30^o. Find x

95^o

100^o

120^o

150^o

View answer & explanation

Correct answer is D

Since ∠QRS = 180^o - 30^o = 150^o and ∠SPQ = ∠QRS (theorem opp. angles in a parallelogram are equal) ∴ x = 150^o

888.

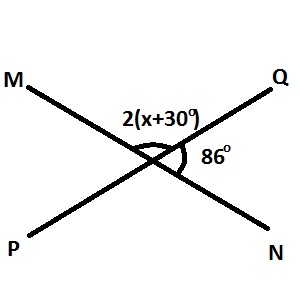
In the diagram PQ and MN are straight lines. Find the value of x

13^o

17^o

28^o

30^o

View answer & explanation

Correct answer is B

The straight line MN = 180 = 2(x+30^o) + 86^o =>
180 = 2x + 60^o + 86^o => 180^o = 2x + 146^o => 2x = 180 - 46 = 34^o => x = 34/2 = 17^o

889.

The probability that John and James pass an examination are 3/4 and 3/5 respectively, find the probability of both boys failing the examination.

$\frac{1}{10}$

$\frac{3}{10}$

$\frac{9}{20}$

$\frac{11}{20}$

View answer & explanation

Correct answer is A

Prob.(John pass) $\frac{3}{4}$ prob.(John fail) $=1-\frac{3}{4}=\frac{1}{4}$
Prob.(James pass) $\frac{3}{5}$ Prob.(James fail) $=1-\frac{3}{5}=\frac{2}{5}$
Prob(both boys fail) $\frac{1}{4}\times \frac{2}{5}=\frac{1}{10}$

890.

The lengths of the adjacent sides of a right - angled triangle are xcm, (x-1)cm. If the length of the hypotenuse is $\sqrt{13}cm$ , find the value of x

View answer & explanation

Correct answer is B

$x^2+(x-1)^2 = (\sqrt{13})^2 \Rightarrow x^2 + x^2 - 2x + 1 = 13\\ 2x^2 - 2x - 12 = 0$ dividing through by 2
$x^2 - x- 6 = 0; (x-3)(x-2) = 0 \Rightarrow x = 3 or -2$