Simplify(0.3 x 105) ÷ (0.4 × 107), leaving you answer in the standard form.
7.5 x 10-4
7.5 x 10-3
7.5 x 10-2
7.5 x 10-1
Correct answer is B
0.3×1050.4×107=3×10−1×1054×10−1×107
3x1044x104
34 x 104-6 = 0.75 x 10-2
= 7.5 x 10-3
Find the LCM of 23 x 3 x 52, 2 x 32 x 5 and 23 x 33 x 5
22 x 33 x 52
23 x 33 x 5
22 x 32 x 52
23 x 33 x 52
Correct answer is D
23 x 3 x 52
2 x 32 x 5
22 x 33 x 5
The L.C.M = 22 x 33 x 52
Evaluate(111two)2 and leave your answer in base 2.
111001two
110001two
101001two
10010two
Correct answer is B
No explanation has been provided for this answer.
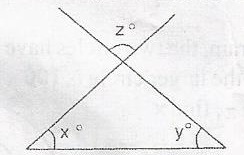
In the diagram what is x + y in terms of z?
180o - z
180o + z
z - 180o
z
Correct answer is A
x + y + z = 180(sum of angles in a △)
x + y = 180 - z
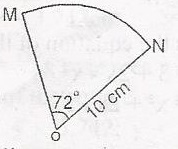
6.28cm
12.6cm
22.6cm
62.8cm
Correct answer is B
Length of arc = θ360×2πr
= 72360×2×227×10cm
= 12.57
= 12.6cm(3 s.f)
WAEC Subjects
Aptitude Tests