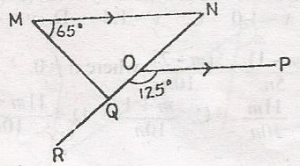
In the diagram, /MN/, /OP/, /QOP/ = 125o. What is the size of < MQR?
11o
120o
130o
160o
Correct answer is B
< NOP = 180 - 125 = 55o(< s on a straight line)
But < NOP = < ONM (alternate < s)
< ONM = 55o
< M + < N + < MQN = 180o (sum of interior < s of a △) i.e
65o + 55o + < MQN = 180
< MQN = 180 - 12o = 60
< MQR + < MQN = 180 (< s on straight line)
< MQR + 60 = 180
< MQR + 60 = 180
< MQR = 180 - 60
= 120o
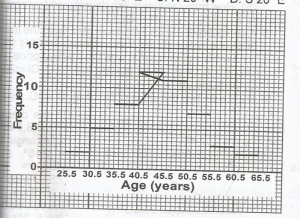
The histogram shows the age distribution of members of a club. What is their modal age?
44.5
42.5
41.5
40.5
Correct answer is A
No explanation has been provided for this answer.
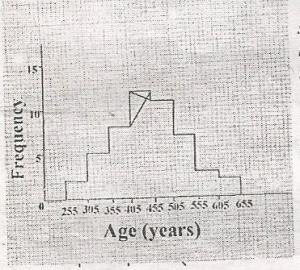
The histogram shows the age distribution of members of a club. How many members are in the club?
52
50
48
40
Correct answer is A
2 + 2 + 5 + 8 + 12 + H + 7 + 3 + 2 = 52
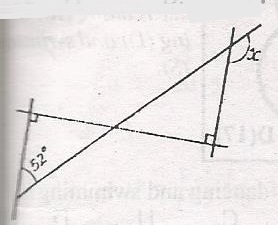
Find the size of the angle marked x in the diagram.
108o
112o
128o
142o
Correct answer is C
x + 52o = 90
x = 90 - 52
x = 38o
k = opposite angle Z
k = 38o
y + k = 90o
y + 38o = 90o
y = 90o - 38o
y = 52o
y = x = 180o(sum of angles on straight line)
52 + x = 180o
x = 180 - 52
x = 128
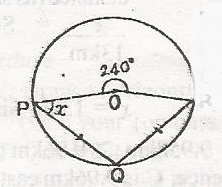
In the diagram, PO and OR are radii, |PQ| = |QR| and reflex < PQR is 240o. Calculate the value x
60o
55o
50o
45o
Correct answer is A
< Q = 2402 (angle at centre twice that at the circumference)
< Q = 120o
Also < POR = 360 - 240
= 120o
( < s at centre) since /PQ/ = /QR/, < x = < R
Byt < x + < R + O + Q = 360 (sum of interior < s of quadrilateral)
x + R + 120 = 360o
x + R = 360 - 240 = 120; Since x = R
x + x = 120
2x = 120
Since x = R
x + x = 120
2x = 120
x = 1202
= 60o
WAEC Subjects
Aptitude Tests