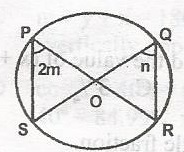
The diagram is a circle centre O. If < SPR = 2m and < SQR = n, express m in terms of n
m = \(\frac{n}{2}\)
m = 2n
m = n - 2
m = n + 2
Correct answer is A
If < SPR = 2m then < SQR = 2m but < AQR was n
n = 2m
m = \(\frac{n}{2}\)
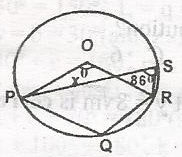
In the diagram, O is a circle centre of the circle PQRS and < PSR = 86o. If < PQR = xo, find x
108o
172o
130o
50o
Correct answer is B
No explanation has been provided for this answer.
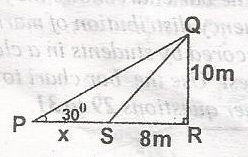
In the diagram, |QR| = 10m, |SR| = 8m
< QPS = 30o, < QRP = 90o and |PS| = x, Find x
1.32m
6.32m
9.32m
17.32
Correct answer is C
In right angled \(\bigtriangleup\)QPR
tan 30o = \(\frac{10}{x + 8}\)
(x + 8) tan 30 = 10
x + 8 = \(\frac{10}{0.5773}\)
x +8 = 17.3
x = 17.3 - 8
x = 9.32
y = kx
y = \(\frac{k}{x}\)
y = k\(\sqrt{x}\)
y = x + k
Correct answer is B
No explanation has been provided for this answer.
Factorise completely: 32x2y - 48x3y3
16x2y(2 - 3xy2)
8xy(4x - 6x2y2)
8x2y(4 - 6xy2)
16xy(2x - 3x2y2)
Correct answer is A
No explanation has been provided for this answer.
WAEC Subjects
Aptitude Tests