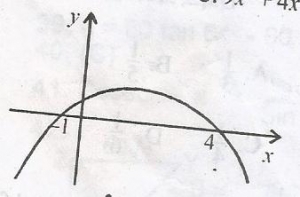
From the diagram above, find the required roots/region of x.
x\(\leq\)-1, x \(\geq\)4
x\(\leq\)4
-1\(\leq\)x\(\leq\)4
x\(\leq\)-1, o\(\leq\)x\(\leq\)4
Correct answer is C
The required roots/region of x is -1\(\leq\)x\(\leq\)4
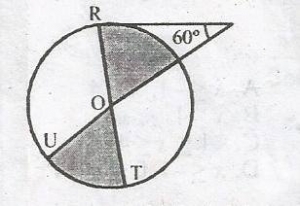
From the diagram above. Find the fraction of the shaded position?
\(\frac{1}{3}\)
\(\frac{1}{5}\)
\(\frac{1}{4}\)
\(\frac{1}{6}\)
Correct answer is D
\(\theta\) = 180o -(90 + 60)
\(\theta\) = 180o - 150o = 30o
Fraction of shaded position = \(\frac{30}{360}\) + \(\frac{30}{360}\)
= \(\frac{1}{12}\) + \(\frac{1}{12}\) = \(\frac{1}{6}\)
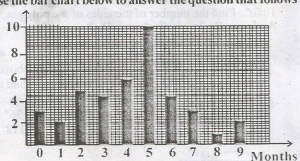
Determine the mean score of the student that took the mathematics test?
4.5
4.3
4.2
4.6
Correct answer is C
(3 x 0) + (1 x 2) + (5 x 2) + (5 x 3) + (5 x 4) +
(10 x 5) + (4 x 6) + (3 x 7) + (1 x 8) + (2 x 9) \(\div\) 40
= \(\frac{168}{40}\) = 4.2
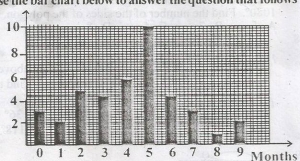
40
30
10
20
Correct answer is A
3 + 2 + 5 + 5 + + 5 + 10 + 4 + 3 + 1 + 2 = 40
Rationalize \(\frac{\sqrt{6} - \sqrt{4}}{\sqrt{6} + \sqrt{4}}\)
5 + 2 \(\sqrt{6}\)
5 - 4 \(\sqrt{6}\)
5 + 4 \(\sqrt{6}\)
5 - 2 \(\sqrt{6}\)
Correct answer is D
\(\frac{\sqrt{6} - \sqrt{4}}{\sqrt{6} + \sqrt{4}}\) = \(\frac{6-2\sqrt{6} - 2\sqrt{6} + 4}{6 - 4}\)
\(\frac{10 - 4\sqrt{6}}{2}\) = 5 - 2\(\sqrt{6}\)
JAMB Subjects
Aptitude Tests