416.
A.
5 + 2 √6
B.
5 - 4 √6
C.
5 + 4 √6
D.
5 - 2 √6
Correct answer is D
√6−√4√6+√4 = 6−2√6−2√6+46−4
10−4√62 = 5 - 2√6
417.
A.
Third quartile range
B.
Semi-quartile range
C.
Cummulative frequency table
D.
Inter-quartile table
Correct answer is B
No explanation has been provided for this answer.
418.
Find the mean of 10, 8, 5, 11, 12, 9, 6, 3, 15, and 23.
A.
11.2
B.
10
C.
10.2
D.
11.3
Correct answer is C
10+8+5+11+12+9+6+3+15+2310
= 10210 = 10.2
419.
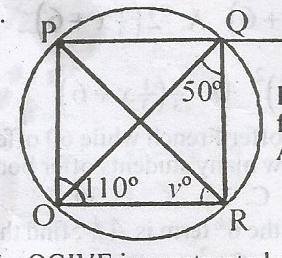

From the cyclic quadrilateral above, find < TSV
A.
60o
B.
80o
C.
70o
D.
50o
Correct answer is B
< TVS = 180o - (80 + 20)
= 180 - 100 = 80o
420.
If Q is a factor of 18 and T is prime numbers between 2 and 18. What is Q∩T?
A.
(2,3)
B.
(2,3,18)
C.
(2,3,9)
D.
(2,3,6)
Correct answer is A
Q = {1,2,3,6,9,18}, T = {2,3,5,7,11,13,17}
Q∩T = {2,3}
JAMB Subjects
Aptitude Tests