Simplify 4\(\sqrt{27}\) + 5\(\sqrt{12}\) − 3\(\sqrt{75}\)
7
− 7
− 7\(\sqrt{3}\)
7\(\sqrt{3}\)
Correct answer is D
4\(\sqrt{27}\) + 5\(\sqrt{12}\) − 3\(\sqrt{75}\)
= 4\(\sqrt{3}\) × 9 + 5\(\sqrt{3}\) × 4 − 3\(\sqrt{3}\) × 25
= 4 × 3\(\sqrt{3}\) + 5 × 2\(\sqrt{3}\) − 3 × 5\(\sqrt{3}\)
= 12\(\sqrt{3}\) + 10\(\sqrt{3}\) − 15\(\sqrt{3}\)
= (12 + 10 − 15)\(\sqrt{3}\)
= 7\(\sqrt{3}\)
23m
25m
20m
22m
Correct answer is C
Capacity = Volume = 3080m3
base diameter = 14m
radius = \(\frac{\text{diameter}}{2}\)
= 7m
Volume of Cylidner = Capacity of cylinder
πr2h = 3080
\(\frac{22}{7}\) × 7 × 7 × h = 3080
h = \(\frac{3080}{22 \times 7}\)
h = 20m
8
6
4
3
Correct answer is B
2x + x = 180o
3x = 180o
x = 60o (exterior angle of the polygon)
angle = \(\frac{\text{total angle}}{\text{number of sides}}\)
60 = \(\frac{360}{n}\)
n = \(\frac{360}{60}\)
n = 6 sides
The value of x + x ( xx) when x = 2 is
16
10
18
24
Correct answer is B
when x=2, we have
\(2 + 2(2^{2})\) = \(2 + 8 = 10\)
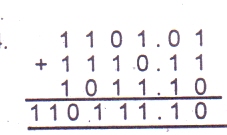
The base in which the operation was performed was
6
2
4
5
Correct answer is B
No explanation has been provided for this answer.
JAMB Subjects
Aptitude Tests