Find the number of ways that the letters of the word EXCELLENCE be arranged
\(\frac{10!}{2!2!2!}\)
\(\frac{10!}{4!2!}\)
\(\frac{10!}{4!2!2!}\)
\(\frac{10!}{2!2!}\)
Correct answer is C
EXCELLENCE
It is a ten letter word = 10!
Since we have repeating letters, we have to divide to remove the duplicates accordingly. There are 4 Es, 2 Cs, 2 Ls
∴ there are
\(\frac{10!}{4!2!2!}\) ways to arrange
60%
32%
25%
20%
Correct answer is C
Total Cost Price = N(250,000 + 70,000)
= N 320,000
Selling Price = N 400,000(Given)
Gain = Selling Price - Cost Price
= 400,000 - 320,000
= 80,000
% gain = \(\frac{\text{Gain}}{\text{Cost Price}}\) × 100
= \(\frac{80,000}{320,000}\) × 100
Gain % = 25%
2x2 -x + 1
2x2 - x -1
2x2 + x + 1
2x2 + x -1
Correct answer is D
by method of long division, we get the answer.
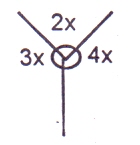
40o
55o
50o
60o
Correct answer is A
Sum of angle at a point = 360o
2x + 3x + 4x = 360
9x = 360
x = \(\frac{360}{9}\)
x = 40o
three times as much
the same
twice as much
half as much
Correct answer is C
Let the speed of the 1st trip be x miles/hr
and the speed of the 2nd trip be 3x miles/hr
Speed = distance/time
∴ Time taken to cover a distance of 50 miles on the 1st trip
= \(\frac{50}{xhr}\)
time taken to cover a distance of 300 miles on the next trip
= \(\frac{300}{3xhr}\)
= \(\frac{100}{xhr}\)
∴the new time compared with the old time is twice as much
JAMB Subjects
Aptitude Tests