What is the loci of a distance 4cm from a given point P?
A straight line of length 4cm
a circle of radius 4cm
perpendicular to point P at 4cm
a circle of diameter 4cm
Correct answer is B
Locus is the path traced at by a point which moves in accordance with a certain law. It is also the set of all possible position occupied by an object The path traced from all possible location of 4cm from a given point P form a circle of radius 4cm with centre P.
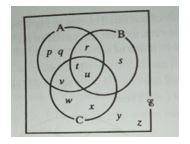
2
3
4
7
Correct answer is C
A = (p, q, r, t, u, v)
B = (r, s, t, u)
A U B = Elements in both A and B = (p, q, r, s, t, u, v)
(A U B)1 = elements in the universal set E but not in (A U B)= (w, x, y, z)
n(A U B) 1 = number of the elements in (A U B)1 = 4

| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 3 | 4 | 5 | 6 | 7 | 6 | 5 | 4 |
How many children are in the hospital
36
40
44
50
Correct answer is B
The total number of students is ∑ f = 3 + 4 + 5 + 6 + 7 + 6 + 5 + 4
= 40
Tanθ is positive and Sinθ is negative. In which quadrant does θ lies
Second only
Third only
Fourth only
First and third only
Correct answer is B
First quadrant: Sin, Cos and Tan are all positive Second quadrant: Sin is positive, Cos is negative and Tan is negative Third quadrant: Tan is positive, Sin is negative and Cos is negative Fourth quadrant: Cos is positive, Sin is negative and Tan is negative The correct option is the third quadrant only where Tanθ is positive and Sinθ is negative
Evaluate log\(_2\) 8 – log\(_3\) \(\frac{1}{9}\)
-1 1\(\frac{1}{2}\)
-1
1
5
Correct answer is D
log\(_2\) 8 – log\(_3\) \(\frac{1}{9}\)
= log \(_2\) 2\(^3\) – log\(_3\) 9\(^{-1}\)
= log\(_2\) 2\(^3\) – log\(_3\) 3\(^{-2}\)
Based on law of logarithm
= 3 log\(_2\) 2 – (-2 log\(_3\) 3)
But log\(_2\) 2 = 1,
log\(_3\) 3 = 1
So, = 3 + 2
= 5
JAMB Subjects
Aptitude Tests