Find the average of the first four prime numbers greater than 10
20
19
17
15
Correct answer is D
Prime numbers are numbers that has only two factors (i.e 1 and itself). They are numbers that are only divisible by 1 and their selves. First four Prime numbers greater than 10 are 11, 13, 17 and 19
Average = sum of numbers / number
= frac(11+13+17+19)4
= 604
= 15
Given that Sin (5x − 28)o = Cos(3x − 50)o, o < x < 90o
Find the value of x
14o
21o
32o
39o
Correct answer is B
Sin(5x - 28) = Cos(3x - 50)………..i
But Sinα = Cos(90 - α)
So Sin(5x - 28) = Cos(90 - [5x - 28])
Sin(5x - 28) = Cos(90 - 5x + 28)
Sin(5x - 28) = Cos(118 - 5x)………ii
Combining i and ii
Cos(3x - 50) = Cos(118 - 5x)
3x - 50 = 118 - 5x
Collecting the like terms
3x + 5x = 118 + 50
8x = 168
x = 1688
x = 21o
Answer is B
What is the loci of a distance 4cm from a given point P?
A straight line of length 4cm
a circle of radius 4cm
perpendicular to point P at 4cm
a circle of diameter 4cm
Correct answer is B
Locus is the path traced at by a point which moves in accordance with a certain law. It is also the set of all possible position occupied by an object The path traced from all possible location of 4cm from a given point P form a circle of radius 4cm with centre P.
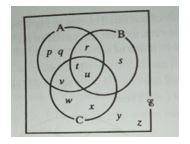
What is n(A U B)1 ?
2
3
4
7
Correct answer is C
A = (p, q, r, t, u, v)
B = (r, s, t, u)
A U B = Elements in both A and B = (p, q, r, s, t, u, v)
(A U B)1 = elements in the universal set E but not in (A U B)= (w, x, y, z)
n(A U B) 1 = number of the elements in (A U B)1 = 4
JAMB Subjects
Aptitude Tests
