Find the equation of the line through the points (5, 7) parallel to the line 7x + 5y = 12.
5x + 7y = 120
7x + 5y = 70
x + y = 7
15x + 17y = 90
Correct answer is B
Equation through (5,7) parallel to the line
7x + 5y = 12
5y = 7x + 12
y = −7x5+125
Gradient = −75
Required equation = y−7x−5=−75
i.e. 5y - 35 = -7x + 35
5y + 7x = 70
| Age in years | 7 | 8 | 9 | 10 | 11 |
| No of pupils | 4 | 13 | 30 | 44 | 9 |
The table above shows the number of pupils in a class with respect to their ages. If a pie chart is constructed to represent the age, the angle corresponding to 8 years old is
48.6°
56.3°
46.8°
13°
Correct answer is C
Total number of pupils : 4 + 13 + 30 + 44 + 9 = 100
The number of 8 - year olds = 13
The angle represented by the 8-year olds on the pie chart = \frac{13}{100} \times 360°
= 46.8°
Find the gradient of the line passing through the points (-2, 0) and (0, -4)
2
-4
-2
4
Correct answer is C
Given (-2, 0) ans (0, -4).
Gradient = \frac{y_2 - y_1}{x_2 - x_1}
= \frac{-4 - 0}{0 - (-2)}
= \frac{-4}{2}
= -2
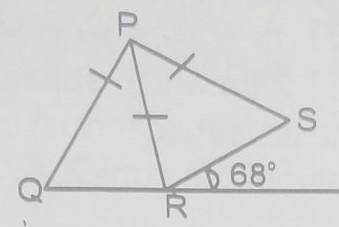
In this fiqure, PQ = PR = PS and SRT = 68^o. Find QPS
136^o
124^o
112^o
68^o
Correct answer is A
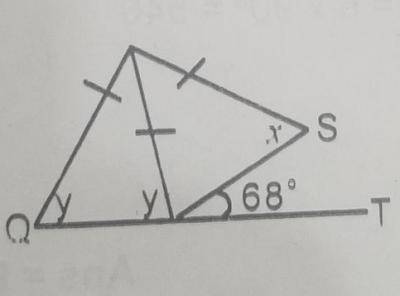
Since PQRS is quadrilateral
2y + 2x + QPS = 360^o
i.e. (y + x) + QPS = 360^o
QPS = 360^o - 2 (y + x)
But x + y + 68^o = 180^o
There; x + y = 180^o - 68^o = 112^o
QPS = 360 - 2(112^o)
= 360^o - 224 = 136^o
JAMB Subjects
Aptitude Tests