JAMB Mathematics Past Questions & Answers

171.

Find the value of x if $\frac{\sqrt{2}}{x + \sqrt{2}}$ = $\frac{1}{x - \sqrt{2}}$

3 $\sqrt{2}$ + 4

3 $\sqrt{2}$ - 4

3 - 2 $\sqrt{2}$

4 + 2 $\sqrt{2}$

View answer & explanation

Correct answer is A

$\frac{\sqrt{2}}{x + 2}$ = x - $\frac{1}{\sqrt{2}}$

x $\sqrt{2}$ (x - $\sqrt{2}$ ) = x + $\sqrt{2}$ (cross multiply)

x $\sqrt{2}$ - 2 = x + $\sqrt{2}$

= x $\sqrt{2}$ - x

= 2 + $\sqrt{2}$

x ( $\sqrt{2}$ - 1) = 2 + $\sqrt{2}$

= $\frac{2 + \sqrt{2}}{\sqrt{2} - 1} \times \frac{\sqrt{2} + 1}{\sqrt{2} + 1}$

x = $\frac{2 \sqrt{2} + 2 + 2 + \sqrt{2}}{2 - 1}$

= 3 $\sqrt{2}$ + 4

172.

If x is positive real number, find the range of values for which $\frac{1}{3x}$ + $\frac{1}{2}$ x = $\frac{2 + 3x}{6x}$ > $\frac{1}{4x}$

x > - $\frac{1}{6}$

x > 0

0 < x < 6

0 < x < $\frac{1}{6}$

View answer & explanation

Correct answer is A

$\frac{1}{3x}$ + $\frac{1}{2}$ x = $\frac{2 + 3x}{6x}$ > $\frac{1}{4x}$

= 4(2 + 3x) > 6x = 12x $^2$ - 2x = 0

= 2x(6x - 1) > 0 = x(6x - 1) > 0

Case 1 (-, -) = x < 0, 6x - 1 > 0

= x < 0, x < $\frac{1}{6}$ (solution)

Case 2 (+, +) = x > 0, 6x - 1 > 0 = x > 0

x > $\frac{1}{6}$

Combining solutions in cases (1) and (2)

= x > 0, x < $\frac{1}{6}$ = 0 < x < $\frac{1}{6}$

173.

The pie chart shows the income of a civil servant in month. If his monthly income is N6,000. Find his monthly basic salary.

N2,050

N2,600

N3,100

N3,450

View answer & explanation

Correct answer is A

360 $^o$ - (60 $^o$ + 60 $^o$ + 67 + 50 = 237 $^o$ )

360 $^o$ - 237 = 130 $^o$

B. Salary = $\frac{123}{360} X \frac{N6000}{1}$

= N2,050

174.

Find the simple interest rate percent annum at which N1000 accumulates to N1240 in 3 years.

10%

12%

View answer & explanation

Correct answer is B

I = $\frac{PRT}{100}$ = 1 = 1240 - 1000 = 240

R = $\frac{240 \times 100}{100 \times 3}$ = 8%

175.

A school boy lying on the ground 30m away from the foot of a water tank towel observes that the angle of elevation of the top of the tank is 60 $^o$ . Calculate the height of the tank.

60 $\sqrt{3m}$

30 $\sqrt{3m}$

20 $\sqrt{3m}$

10 $\sqrt{3m}$

View answer & explanation

Correct answer is B

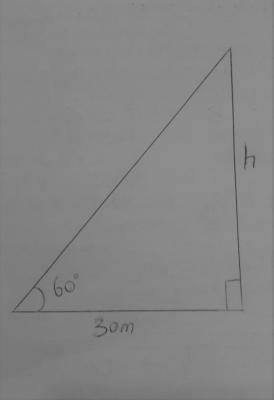
h = 30 tan 60

= 30 $\sqrt{3}$

JAMB Subjects

Literature in English

Islamic Religious Knowledge

Christian Religious Knowledge

Aptitude Tests

Microsoft Office Questions and Answers

Typing Speed and Accuracy Test

Quantitative Reasoning Questions and Answers

Abstract Reasoning Questions and Answers

Puzzles Questions and Answers

Situational Judgement Questions and Answers

Spatial Reasoning Questions and Answers

Logical Reasoning Questions and Answers

Numerical Reasoning Questions and Answers

Personality Test

Nigeria General Knowledge Questions and Answers

Verbal Reasoning Questions and Answers

Data Interpretation Questions and Answers

See all →

View latest jobs in Nigeria today

JAMB Mathematics Past Questions & Answers - Page 35

JAMB Subjects

Aptitude Tests