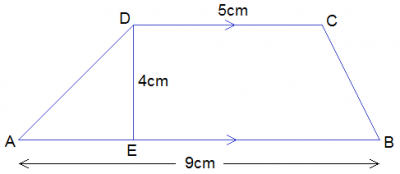
13 cm
4 cm
6 cm
7 cm
Correct answer is A
Area of Trapezium = 1/2(sum of parallel sides) * h
91 = 12 (5 + 9)h
cross multiply
91 = 7h
h = 917
h = 13cm
Determine the maximum value of y=3x2 + 5x - 3
6
0
2
No correct option
Correct answer is D
y=3x2 + 5x - 3
dy/dx = 6x + 5
as dy/dx = 0
6x + 5 = 0
x = −56
Maximum value: 3 2−56 + 5 −56 - 3
3 7536 - 256 - 3
Using the L.C.M. 36
= 25−50−3636
= −6136
No correct option
Solve the following equation: 2(2r−1) - 53 = 1(r+2)
( -1,52 )
( 1, - 52 )
( 52, 1 )
(2,1)
Correct answer is B
2(2r−1) - 53 = 1(r+2)
2(2r−1) - 1(r+2) = 53
The L.C.M.: (2r - 1) (r + 2)
2(r+2)−1(2r−1)(2r−1)(r+2) = 53
2r+4−2r+1(2r−1)(r+2) = 53
cross multiply the solution
3 * 5 = (2r - 1) (r + 2) * 5
divide both sides 5
3 = 2r2 + 3r - 2 (when expanded)
collect like terms
2r2 + 3r - 2 - 3 = 0
2r2 + 3r - 5 = 0
Factors are -2r and +5r
2r2 -2r + 5r - 5 = 0
[2r2 -2r] [+ 5r - 5] = 0
2r(r-1) + 5(r-1) = 0
(2r+5) (r-1) = 0
r = 1 or - 52
If 7 + y = 4 (mod 8), find the least value of y, 10 ≤y≤30
11
13
19
21
Correct answer is B
7 + y = 4 (mod 8)
y = 4 - 7 (mod 8)
y = -3 + 8 (mod 8)
y = 5 + 8 (mod 8)
y = 13
JAMB Subjects
Aptitude Tests