JAMB Mathematics Past Questions & Answers - Page 274

1,366.

If three angles of a quadrilateral are (3y - x - z)^o, 3x^o, (2z - 2y - x)^o find the fourth angle in terms of x, y and z

(360 - x- y - z)^o

(360 + x + y - z)^o

(180 - x + y + z)^o

View answer & explanation

Correct answer is A

The sum of angles of a quadrilateral is 360^o

∴ (3y - x - z)^o + 3x^o + (2z - 2y - x)^o + p^o = 360^o

Where P is the fourth angle

3y - x - z + 3x + 2z - 2y - x + p = 360^o

p = 360 - (x + y + z)

∴ p = (360 - x - y - z)^o

1,367.

\(\begin{array}{c|c} \text{Age in years} & 10 & 11 & 12 \\ \hline \text{Number of pupils} & 6 & 27 & 7\end{array}\)
The table above shows the number of pupils in each age group in a class. What is the probability that a pupil chosen at random is at least 11 years old?

\(\frac{27}{40}\)

\(\frac{17}{20}\)

\(\frac{33}{40}\)

\(\frac{3}{20}\)

View answer & explanation

Correct answer is B

Total number of pupils = 7 + 27 + 6 = 40

n(at least 11 years old) = 27 + 7 = 34.

P(picking a pupil who is at least 11 years old) = \(\frac{34}{40} = \frac{17}{20}\).

1,368.

The determination of the matrix \(\begin{pmatrix} 1 & 3 & 3 \\ 4 & 5 & 6\\ 2 & 0 & 1 \end{pmatrix}\) is

-67

-57

-1

View answer & explanation

Correct answer is C

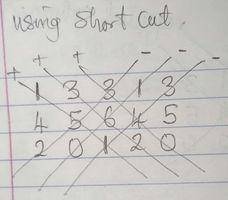
((1 x5x1) +( 3x6x2) + (3x4x0)) - ((3x5x2) + (1x6x0) + (3x4x1))

( 5 + 36) - (30 +12) = 41 - 42

= -1

1,369.

Solve for x and y \(\begin{pmatrix} 1 & 1 \\ 3 & y \end{pmatrix}\)\(\begin{pmatrix} x \\ 1 \end{pmatrix}\) = \(\begin{pmatrix} 4 \\ 1\end{pmatrix}\)

x = 3, y = 8

x = 3, y = -8

x = -8, y = 3

x = 8, y = -3

View answer & explanation

Correct answer is B

\(\begin{pmatrix} 1 & 1 \\ 3 & y \end{pmatrix}\)\(\begin{pmatrix} x \\ 1 \end{pmatrix}\) = \(\begin{pmatrix} 4 \\ 1\end{pmatrix}\) = x + 1 = 4

x = 4 - 1

= 3

3x + y =1

3(3) = y = 1

= 9 + y = 1

y = 1 - 9

= -8