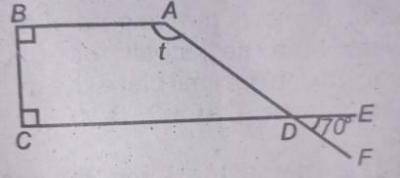
In the diagram, ∠ABC and ∠BCD are right angles, ∠BAD = t and ∠EDF = 70°. Find the value of t.
70°
165°
140°
110°
Correct answer is D
Vertically opp angles are equal ∠CDE = 70°
Sum of interior angles in a quadilateral = 360°
(90 + 90 + 70 + t)° = 360°
t° = 360° - 250°
t° = 110°
3 years
10 years
5 years
15 years
Correct answer is C
Mensah’s age is 5. Thus,
Joyce’s age is 15 (5*3=15)
The difference between their ages is 10 (15–5=10)
As we ought to find how many years Joyce’s age will be twice of Mensah’s age, we should write down the following :
15+X=2*(5+X)
15+X=10+2X lets add (-10-X) to both sides of the equation and
15+X-10-X = 10+2X-10-X
5=X —-> X=5
After 5 years Joyce’s age will be 20 (15+5=20)
After 5 years Mensah’s age will be 10 (5+5=10)
After 5 years Joyce will be twice as old as Mensah (10*2=20)
\(\frac{1}{3}\)
1\(\frac{1}{2}\)
1\(\frac{1}{6}\)
\(\frac{1}{2}\)
Correct answer is B
The sum of 2 \(\frac{1}{6}\) and 2\(\frac{7}{12}\)
= \(\frac{13}{6}\) + \(\frac{31}{12}\)
= \(\frac{13 \times 2 + 31}{12}\)
= \(\frac{26 + 31}{12}\)
= \(\frac{57}{12}\)
What should be subtracted from \(\frac{57}{12}\) to give 3\(\frac{1}{4}\)
\(\frac{57}{12}\) - y = 3\(\frac{1}{4}\)
: y = \(\frac{57}{12}\) - 3\(\frac{1}{4}\) = \(\frac{57}{12}\) - \(\frac{13}{4}\)
y = \(\frac{57 - 3 \times 13}{12}\) = \(\frac{57 - 39}{12}\)
y = \(\frac{18}{12}\)
y = \(\frac{3}{2}\) or 1\(\frac{1}{2}\)
3(r -p)(2q + s)
3(p + r)( 2q - 2q - s)
3(2q - s)(p + r)
3(r - p)(s - 2q)
Correct answer is C
6pq-3rs-3ps+6qr = 3 (2pq - rs - ps + 2qr)
= 3 ({2pq + 2qr} {-ps - rs})
= 3 (2q{ p + r} -s{p + r})
= 3 ({2q - s}{p + r})
Find the 5th term of the sequence 2,5,10,17....?
22
24
36
26
Correct answer is D
Simply add odd number starting from '3' to the next number
2
2 + 3 = 5
5 + 5 = 10
10 + 7 = 17
17 + 9 = 26
The fifth term = 26
JAMB Subjects
Aptitude Tests