25cm
18cm
36cm
29cm
25.5cm
Correct answer is A
Circumference of PRS = \(\frac{\pi}{2}\) = \(\frac{22}{7}\) x \(\frac{7}{1}\) x \(\frac{1}{2}\)
= 11cm
Side PT = 7cm, Side TR = 7cm
Perimeter(PTRS) = 11cm + 7cm + 7cm
= 25cm
Simplify \(\sqrt[3]{\frac{27a^{-9}}{8}}\).
\(\frac{9a^2}{2a^3}\)
\(\frac{3}{2a^3}\)
\(\frac{2}{3a^2}\)
\(\frac{3a^2}{2}\)
Correct answer is B
\(\sqrt[3]{\frac{27a ^{-9}}{8}}\) = \(\frac{3a^{-3}}{2}\)
= \(\frac{3}{2}\) x \(\frac{1}{a^3}\)
= \(\frac{3}{2a^3}\)
6.00cm2
6.10cm2
6cmv
6.09cm2
4.00cm2
Correct answer is B
Area of the paper = area of square = L x B or S2
where s = S x k
Area of the paper = (2.524)2
area of the diagram = (0.524)2
area not covered = (2.524)2 - (0.524)2
= 6.370576 - 0.274576
= 6.096
= 6.10cm2 (2 s.f)
4
3
5
4.5
None
Correct answer is A
\(\begin{array}{c|c} x & f \\\hline 1 & 3\\ 2 & 13\\3 & 15\\ 4 & 28\\ 5 & 21\\ 6 & 10\\ 7 & 7\\ 8 & 4\end{array}\)
Median is half of total frequency = 50th term
4 falls in the range = 4
20o 34'
243o 26'
116o 34'
63o 26'
240o 56'
Correct answer is B
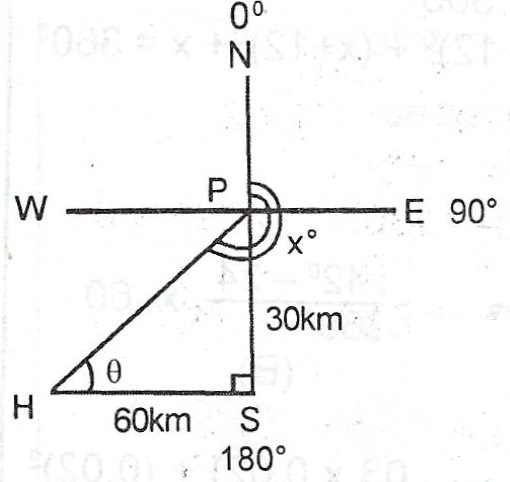
Let the bearing of H from P be represented by x°.
\(\tan \theta = \frac{30}{60} = 0.5\)
\(\theta = \tan^{-1} (0.5) = 26.565°\)
\(x = 180° + (90 - 26.565)\)
\(x = 180 + 63.435 = 243.435°\)
= \(243° 26'\)
JAMB Subjects
Aptitude Tests