215 and 88
91 and 227
227 and 91
92 and 238
Correct answer is C
- Alpha radiation consists of helium- He42
2 Alpha decay --> 2 X He42 = Element84
- Beta particles are high energy electrons- e0−1
3 Beta particles --> 3 X e0−1 = Element0−3
- Gamma rays are waves of electromagnetic energy, or photons.
the mass and atomic number of the resulting element = U23592 - Elements( 84 + 0−3 )
--> Element22791
An object is weighed at different locations on the Earth. What will be the right observation?
Both the mass and weight vary
The weight is constant while the mass varies
The mass is constant while the weight varies
Both the mass and weight are constant
Correct answer is C
No explanation has been provided for this answer.
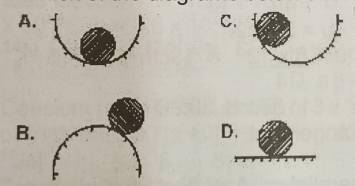
A
B
C
D
Correct answer is D
Neutral Equilibrium: If the body neither returns to its original position nor increases its displacement further, it will simply adopt its new position.
Examples of neutral equilibrium
- Ball moving on the ground.
- Motion of sphere.
- A roller.
- A pencil lying horizontally.
- An egg lying horizontally on a flat surface.
2700
450
900
1800
No Correct Option
Correct answer is C
Comparing y=10Sin(1000πt−πx34) with y = A sin (ωt - ϕ)
where ϕ = \frac{2\pi x}{λ}
comparing: \frac{2\pi x}{λ} = \frac{\pi x}{34}
λ = 34 \times 2 = 68
: ϕ = \frac{2\pi x}{λ} = \frac{2\pi \times 153}{68}
ϕ = 4.5\pi rad = 810° or 90°
since sin 810° or 90° = 1
JAMB Subjects
Aptitude Tests