666.
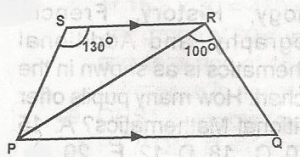
< PQR + 130o = 180
< PQR = 180 - 130

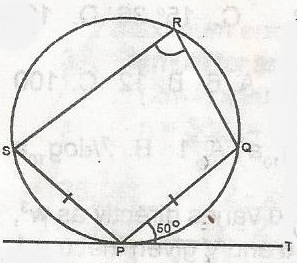
In the diagram, if PS = SR and PQ||SQ, what is the size of PQR?
A.
25o
B.
50o
C.
55o
D.
65o
E.
75o
Correct answer is B
Explanation
< PQR + , PSR 180(Opposite angles in a Quadrilateral are supplementary)< PQR + 130o = 180
< PQR = 180 - 130
667.
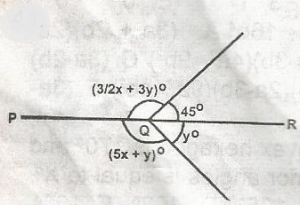

In the figure, PQR is a straight line. Find the values of x and y
A.
x = 22.5o, y = 33.75o
B.
x = 15o, y = 52.5o
C.
x = 22.5o, y = 45.0o
D.
x = 56.25o, y = 11.5o
Correct answer is A
32x + 3y + 45° = 180°
3x + 6y + 90° = 360°
3x + 6y = 270.......(i) x 2,
5x + y + y = 180°
5x + 2y = 180° ... (ii) x 6
6x + 12y = 540 ... (iii)
30x + 12y = 1080 ... (iv)
eqn(iv) - eqn(iii)
24x = 540
x = 22.5° and y = 33.75°
670.
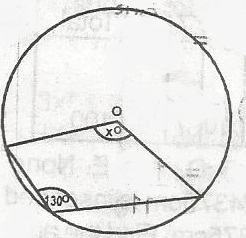

If O is the centre of the circle in the figure, find the value of x
A.
50
B.
260
C.
100
D.
65
E.
130
Correct answer is C
From the diagram; The value of x = 360o - 2(130o)
= 360 - 260
= 100o
JAMB Subjects
Aptitude Tests