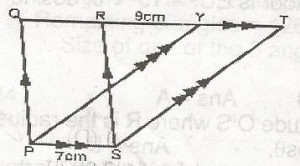
56cm2
112cm2
120cm2
176cm2
Correct answer is C
From the figure, PS = QR = YT = 7cm
Area of parallelogram PQRS = 56cm
56 = base x height, where base = 7
7 x h = 56cm,
h = \(\frac{56}{7}\)
= 8cm
Area of trapezium \(\frac{1}{2}\) (sum of two sides)x height where two sides are QT and PS but QT = QR + RY + YT = 7 +9 + 7 = 23cm
Area of trapezium PQTS = \(\frac{1}{2}\)(23 + 7) x 8
\(\frac{1}{2}\) x 30 x 8 = 120cmsq
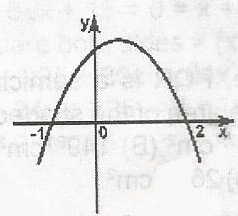
What is the equation of the quadratic function represented by the graph?
y = x2 + x - 2
y = -x2 - x + 2
y = x2 - x - 2
y = -x2 - x + 2
Correct answer is C
The required equation is y = x2 - x - 2
i.e. B where the graph touches the graph touches the x-axis y = 0
x2 - x - 2 = 0 = (x + 1)(x - 2) = 0
Hence roots of the equation are -1 and 2 as shown in the graph
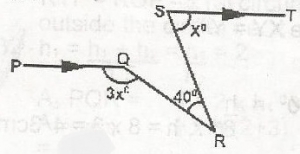
In the figure, PQ is a parallel to ST and QRS = 40o. Find the value of x
55o
60o
65o
75o
Correct answer is A
From the figure, 3x + x - 40o = 180o
4x = 180o + 40o
4x = 220o
x = \(\frac{220}{4}\)
= 55o
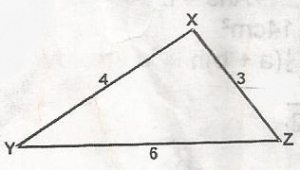
In \(\bigtriangleup\)XYZ, determine the cosine of angle Z.
\(\frac{3}{39}\)
\(\frac{29}{36}\)
\(\frac{14}{5}\)
\(\frac{7}{5}\)
Correct answer is B
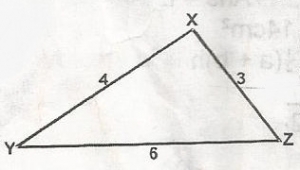
cos z = \(\frac{y^2 + x^2 -z^2}{2yx}\)
= \(\frac{9 + 36 - 16}{2(3)(6)}\)
= \(\frac{29}{36}\)
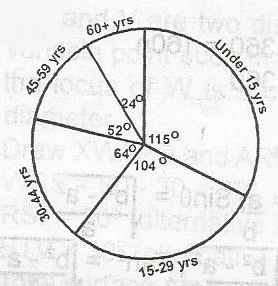
29 x 104
26 x 104
16 x 104
13 x 104
Correct answer is B
15 - 29 years is represented by 104o
Number of people in the group is \(\frac{104}{360}\) x 0.9m
= 260000 = 26 x 104
JAMB Subjects
Aptitude Tests