1, 3, 2
0, 0, 0
0, 2, 3
1, 2, 3
Correct answer is D
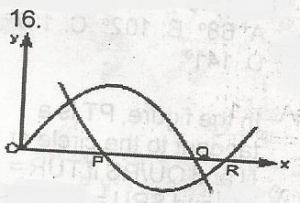
The two equations are y = x(2 - x) and y = (x - 1)(x - 3)
The root of these equations are points where the graph of the equations cuts the x axis; but at these points = 0
put y = 0; 0 = x(2 - x)
0 = (x - 1)(x - 3)
x = 0 or x = 2; x = 1 or x = 3
The values of x at P, Q, R are increasing towards the positive direction of x-axis
at P, x = 1 at Q, x = 2 at R, x = 3
P, Q, R are respectively (1, 2, 3)
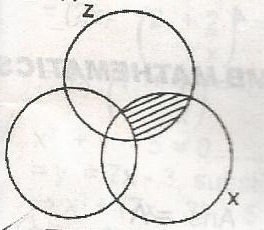
The shaded portion in the venn diagram is
x \(\cap\) z
xo \(\cap\) y \(\cap\) z
x \(\cap\) yo \(\cap\) z
x \(\cap\) y \(\cap\) zo
Correct answer is C
The shaded part exists on x \(\cap\) z but not in y
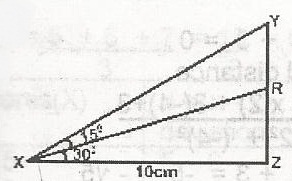
In the figure, if XZ is 10cm, calculate RY in cm
10
10(1 - \(\frac{1}{\sqrt{3}}\))
10(1 - \(\frac{1}{\sqrt{2}}\))
10[1 - \(\sqrt{3}\)]
Correct answer is B
RY = YZ - RZ
= 10 tan 45 - 10 tan 30
= 10(1 - \(\frac{1}{\sqrt{3}}\))
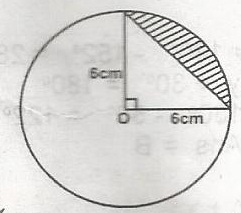
The diagram is a circle with centre O. Find the area of the shaded portion
9(\(\pi - 2) cm^2\)
18\(\pi cm^2\)
9\(\pi cm^2\)
36\(\pi cm^2\)
Correct answer is A
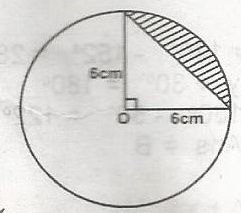
Area of the quadrant = \(\frac{1}{4} \pi r^2 = \frac{1}{4} \pi (6)^2\)
= \(\frac{36 \pi}{4} = 9 \pi \)
Area of the triangle = \(\frac{1}{2} \times 6 = 18 \times \sin 90^o = 18\)
Area of shaded portion =(9 \(\pi \) - 18)cm^2\) =
9(\(\pi - 2)cm^2\).
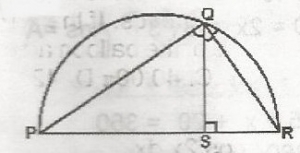
QS = PS\(\sqrt{SR}\)
QS = \(\sqrt{(PS SR)}\)
QS = 2\(\sqrt{(PS SR)}\)
QS = \(\frac{1}{\sqrt{2}}\)\(\sqrt{(PS SR)}\)
Correct answer is B
No explanation has been provided for this answer.
JAMB Subjects
Aptitude Tests