Loading [MathJax]/jax/output/HTML-CSS/jax.js

JAMB Mathematics Past Questions & Answers - Page 116

576.

The figure shows circles of radii 3cm and 2cm with centres at X and Y respectively. The circles have a transverse common tangent of length 25cm. Calculate XY

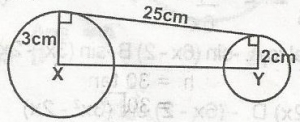
$\sqrt{630}$ cm

$\sqrt{626}$ cm

$\sqrt{615}$ cm

$\sqrt{600}$ cm

View answer & explanation

Correct answer is B

No explanation has been provided for this answer.

577.

The mean and the range of the set of numbers 1, 20, 1.00, 0.90, 1.40, 0.80, 1.20 and 1.10 are me and r

1.11

1.65

1.85

2.45

View answer & explanation

Correct answer is B

m = 1.05, r = 0.6 m + r = 1.05 + 0.5 = 1.65

578.

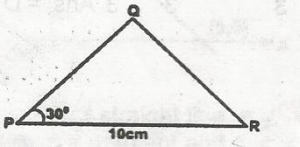
In the diagram, find PQ if the area of triangle PQR is 35cm $^2$

7cm

10cm

14cm

17cm

View answer & explanation

Correct answer is A

PQ x 10 sin 30 = 35

PQ = $\frac{35}{10 \sin 30}$

= 7cm

579.

In the diagram, the base diameter is 14cm while the height is 12cm. Calculate the total surface area if the cylinder has both a base and a top.[ $\pi \frac{22}{7}$ ]

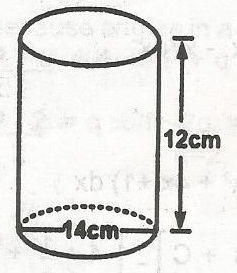
836cm²

308cm²

528cm²

154cm²

View answer & explanation

Correct answer is A

Area(S) = 2 $\pi r^2 + 2 \pi rh = 2\pi r(h + r)$

D = 14cm, 2r = D

r = $\frac{D}{2}$

= 7cm

S = 2 x $\frac{22}{7} \times [7 + 12] = 44 \times 19$

= 836cm²

580.

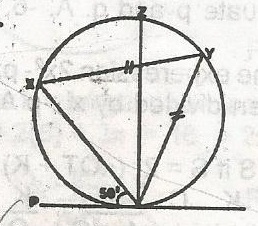
PT is a tangent to the circle TYZX. YT = YX and < PTX = 50^o. Calculate < TZY

50^o

65^o

85^o

130^o

View answer & explanation

Correct answer is B

XTY = 50^o = TXY = $\frac{130^o}{2}$

= 65^o

JAMB Subjects

Literature in English

Islamic Religious Knowledge

Christian Religious Knowledge

Aptitude Tests

Microsoft Office Questions and Answers

Quantitative Reasoning Questions and Answers

Verbal Reasoning Questions and Answers

Situational Judgement Questions and Answers

Nigeria General Knowledge Questions and Answers

Numerical Reasoning Questions and Answers

Logical Reasoning Questions and Answers

Spatial Reasoning Questions and Answers

Typing Speed and Accuracy Test

Personality Test

Data Interpretation Questions and Answers

Puzzles Questions and Answers

Abstract Reasoning Questions and Answers

See all →

View latest jobs in Nigeria today