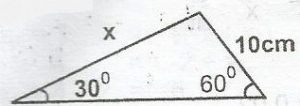
Find the value of x in the figure above
20√3cm
10√3cm
5√3cm
4√3cm
Correct answer is B
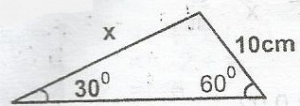
In the figure above, xsin60o=10sin30o (Sine rule)
x = 10sin60osin30o
= 10 x √32×12
= 10 x √32×21
= 10√3cm
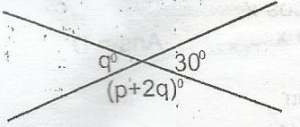
From the figure above, what is the value of p?
135o
90o
60o
45o
Correct answer is B
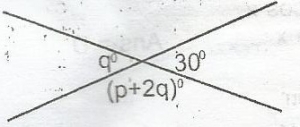
In the figure above, qo = 30o (vertically opposite angles)
(P + 2q)o + 30o = 180o(angles on a straight line)
p + 2 x 30o + 30o = 180o
p + 60o + 30o = 180o
p + 90o = 180o
p = 180o - 90o
= 90o
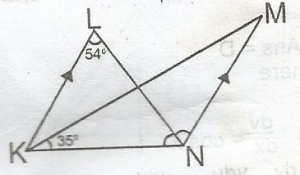
91o
89o
37o
19o
Correct answer is C
In the diagram above, α = 54o(alternate angles; KL||MN) < KNM = 2α (LN is bisector of < KNM) = 108o
35o + < KMN + 108o = 180o(sum of angles of △)
< KMN + 143o = 180o
< KMN = 180o - 143o
= 37o
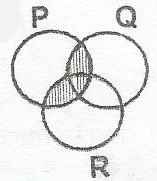
From the venn diagram above, the shaded parts represent
(P∩Q)∪(P∩R)
(P∪Q)∩(P∩R)
(P∪Q)∪(P∪R)
(P∩Q)∪(P∪R)
Correct answer is A
No explanation has been provided for this answer.
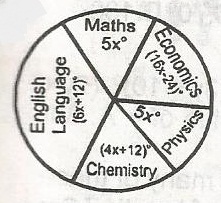
30
11
50
20
Correct answer is B
5x° + (16x - 24)° + 5x° + (4x + 12)° + (6x + 12)° = 360°
36x° - 24 + 12 + 12 = 360°
36x° = 360°
x° = \frac{360°}{36}
= 10°
Thus, the angle of sector representing Mathematics is 5 x 10° = 50°. Hence the number of students who offer mathematics is
\frac{50}{360} \times 80 \approx 11
JAMB Subjects
Aptitude Tests