In the diagram above, PQT is an isosceles triangle.|PQ| =...
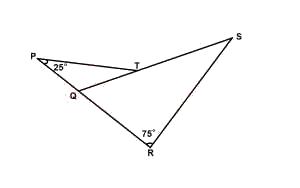
In the diagram above, PQT is an isosceles triangle.|PQ| = |QT|, ∠SRQ = 75°, ∠QPT = 25° and PQR is straight line. Find ∠RST
20o
50o
55o
70o
75o
Correct answer is C
< PTQ = 25° (base angles of an isos. triangle)
∴ < PQT = 180° - (25° + 25°) = 130° (sum of angles in triangle PQT)
\therefore < RST = 130° - 75° = 55° (exterior angle = sum of 2 opp. interior angles)
Similar Questions
Find the value of x and y respectively if 3x - 5y + 5 = 0 and 4x - 7y + 8 = 0 ...
Simplify 2.04 × 3.7 (Leave your answer in 2 decimal place) ...
TQ is tangent to circle XYTR, < YXT = 32o, RTQ = 40o. find < YTR ...
Expand the expression(3a - xy)(3a + xy) ...
The graph of y = ax^2 + bx + c is shown oon the diagram. Find the minimum value of y...
From the equation whose roots are x = \frac{1}{2} and -\frac{2}{3}...